Euler-Bernoulli Kiriş Teorisi
Euler-Bernoulli kiriş teorisi (mühendis kiriş teorisi veya klasik kiriş teorisi olarak da bilinir), bir yük uygulandığında kirişlerin eğilmesini hesaplamak için basit bir yöntemdir. Bu, kesme deformasyonlarının etkilerini dikkate almadan bir kirişin küçük sapmaları (bir şeyin ne kadar hareket ettiği) için geçerlidir. Bu nedenle, Timoshenko kiriş teorisinin özel bir durumu olarak düşünülebilir. İlk olarak 1750 civarında ortaya atılmıştır. Eiffel Kulesi ve dönme dolabın 19. yüzyılın sonlarında geliştirilmesi sırasında popülerlik kazanmıştır. Bundan sonra, makine mühendisliği ve inşaat mühendisliği de dahil olmak üzere birçok mühendislik alanında kullanılmıştır. Diğer gelişmiş yöntemler geliştirilmiş olsa da, Euler-Bernoulli kiriş teorisi basitliği nedeniyle hala yaygın olarak kullanılmaktadır.
Euler-Bernoulli'nin kiriş teorisi kullanılarak tahmin edilebilen kirişlerin bükülmesini gösteren titreşimli bir cam kiriş.
Tarih
Leonhard Euler ve Daniel Bernoulli 1750 yılında teoriyi bir araya getiren ilk kişiler olmuştur. O dönemde bilim ve mühendislik bugünkünden farklı görülüyordu. Euler-Bernoulli Kiriş teorisi gibi matematiksel teorilere pratik mühendislik kullanımı için güvenilmiyordu. Köprüler ve binalar 19. yüzyılın sonlarına kadar aynı yöntemler kullanılarak tasarlanmaya devam etti. Eyfel Kulesi ve dönme dolap, teorinin geçerliliğini daha büyük ölçekte gösterdi.
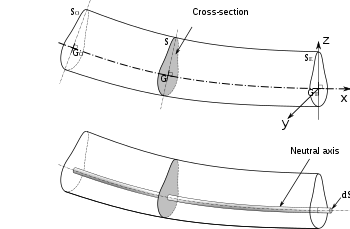
Eğilmiş bir kirişin tarafsız eksenini gösteren kesit çizimi
Statik kiriş denklemi
Euler-Bernoulli denklemi, kirişin sapması ile uygulanan yük arasındaki ilişkiyi aşağıda gösterildiği gibi açıklar:
d 2 d x 2 ( E I d 2 w d x 2 ) = q {\displaystyle {\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}\left(EI{\frac {\mathrm {d} ^{2}w}{\mathrm {d} x^{2}}}\right)=q\,} 
Burada w ( x ) {\displaystyle w(x)}
, x {\displaystyle x}
konumunda kirişin z {\displaystyle z}
yönündeki sapmasını tanımlar. q {\displaystyle q}
yayılı bir yüktür, başka bir deyişle birim uzunluk başına bir kuvvettir (alan başına bir kuvvet olan basınca benzer şekilde); x {\displaystyle x} , w {\displaystyle w} 'nin bir fonksiyonu olabilir. 
veya diğer değişkenler.
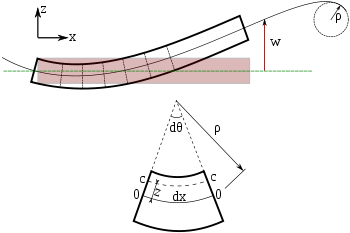
Bir Euler-Bernoulli kirişinin bükülmesi. Kirişin her bir kesiti tarafsız eksene 90 derecedir.
Sorular ve Yanıtlar
S: Euler-Bernoulli kiriş teorisi nedir?
C: Euler-Bernoulli kiriş teorisi, kesme deformasyonlarının etkilerini dikkate almadan, bir yük uygulandığında kirişlerin eğilmesini hesaplamak için kullanılan basit bir yöntemdir.
S: Euler-Bernoulli kiriş teorisi ilk olarak ne zaman ortaya atılmıştır?
C: Euler-Bernoulli kiriş teorisi ilk olarak 1750 civarında ortaya atılmıştır.
S: Euler-Bernoulli kiriş teorisi Eyfel Kulesi ve dönme dolabın geliştirilmesinde kullanıldı mı?
C: Evet, Euler-Bernoulli kiriş teorisi 19. yüzyılın sonlarında Eyfel Kulesi ve dönme dolabın geliştirilmesi sırasında popülerlik kazanmıştır.
S: Euler-Bernoulli kiriş teorisinin kullanıldığı bazı mühendislik alanları nelerdir?
C: Euler-Bernoulli kiriş teorisi, makine mühendisliği ve inşaat mühendisliği de dahil olmak üzere birçok mühendislik alanında kullanılmıştır.
S: Euler-Bernoulli kiriş teorisi günümüzde hala yaygın olarak kullanılıyor mu?
C: Evet, Euler-Bernoulli kiriş teorisi, diğer gelişmiş yöntemler geliştirilmiş olsa da, basitliği nedeniyle günümüzde hala yaygın olarak kullanılmaktadır.
S: Euler-Bernoulli kiriş teorisi bir kirişte ne tür sapmalar için geçerlidir?
C: Euler-Bernoulli kiriş teorisi bir kirişteki küçük sapmalar için geçerlidir.
S: Euler-Bernoulli kiriş teorisi kayma deformasyonlarının etkilerini dikkate alır mı?
C: Hayır, Euler-Bernoulli kiriş teorisi kayma deformasyonlarının etkilerini dikkate almaz.
