Doğrusal regresyon
Doğrusal regresyon, bağımlı bir değişken ile bir veya daha fazla açıklayıcı değişken arasındaki ilişkiyi düz bir çizgi kullanarak açıklamanın bir yoludur. Regresyon analizinin özel bir durumudur.
Doğrusal regresyon, üzerinde titizlikle çalışılan ilk regresyon analizi türüdür. Bunun nedeni, bilinmeyen parametrelerine doğrusal olarak bağlı olan modellerin, parametrelerine doğrusal olarak bağlı olmayan modellere göre daha kolay uydurulabilmesidir. Dahası, elde edilen tahmin edicilerin istatistiksel özelliklerinin belirlenmesi daha kolaydır.
Doğrusal regresyonun birçok pratik kullanımı vardır. Çoğu uygulama aşağıdaki iki geniş kategoriden birine girer:
- Doğrusal regresyon, bir dizi gözlenen değere (veriye) bir tahmin modeli uydurmak için kullanılabilir. Amaç tahmin, öngörü veya azaltma ise bu kullanışlıdır. Böyle bir model geliştirildikten sonra, X'in ek bir değeri, beraberinde y değeri olmadan verilirse, uydurulan model y değerinin tahmininde kullanılabilir.
- Bir y değişkeni ve y ile ilişkili olabilecek bir dizi X1 , ..., Xp değişkeni verildiğinde, y ile Xj arasındaki ilişkinin gücünü ölçmek, hangi Xj değişkeninin y ile hiçbir ilişkisi olmadığını değerlendirmek ve Xj değişkeninin hangi alt kümelerinin y hakkında gereksiz bilgi içerdiğini belirlemek için doğrusal regresyon analizi uygulanabilir.
Doğrusal regresyon modelleri, doğru ile veri noktaları (örneğin artıklar) arasındaki dikey mesafeyi mümkün olduğunca küçük yapmaya çalışır. Buna "doğruyu veriye uydurmak" denir. Genellikle, doğrusal regresyon modelleri artıkların karelerinin toplamını (en küçük kareler) en aza indirmeye çalışır, ancak başka uydurma yolları da mevcuttur. Bunlar arasında başka bir normda "uyum eksikliğini" en aza indirmek (en küçük mutlak sapmalar regresyonunda olduğu gibi) veya ridge regresyonunda olduğu gibi en küçük kareler kayıp fonksiyonunun cezalandırılmış bir versiyonunu en aza indirmek yer alır. En küçük kareler yaklaşımı, doğrusal olmayan modelleri uydurmak için de kullanılabilir. Yukarıda belirtildiği gibi, "en küçük kareler" ve "doğrusal model" terimleri yakından bağlantılıdır, ancak eş anlamlı değildir.
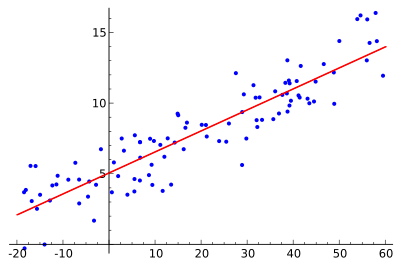
Buradaki fikir kırmızı eğriyi bulmaktır, mavi noktalar gerçek örneklerdir. Doğrusal regresyon ile tüm noktalar tek bir düz çizgi kullanılarak bağlanabilir. Bu örnekte, kırmızı çizgi ile her bir örnek noktası arasındaki mesafenin karesinin minimize edildiği basit doğrusal regresyon kullanılmaktadır.
Kullanım
Ekonomi
Doğrusal regresyon, ekonomideki temel analitik araçtır. Örneğin, tüketim harcamalarını, sabit yatırım harcamalarını, stok yatırımlarını, bir ülkenin ihracat alımlarını, ithalat harcamalarını, likit varlık bulundurma talebini, işgücü talebini ve işgücü arzını tahmin etmek için kullanılır.
Sorular ve Yanıtlar
S: Doğrusal regresyon nedir?
C: Doğrusal regresyon, matematik kullanarak başka şeyler değiştiğinde bir şeyin nasıl değiştiğine bakmanın bir yoludur. "Regresyon çizgisi" olarak bilinen düz bir çizgi oluşturmak için bağımlı bir değişken ve bir veya daha fazla açıklayıcı değişken kullanır.
S: Doğrusal regresyonun avantajları nelerdir?
C: Bilinmeyen parametrelerine doğrusal olarak bağlı olan modellerin uydurulması, parametrelerine doğrusal olarak bağlı olmayan modellere göre daha kolaydır. Ayrıca, elde edilen tahmin edicilerin istatistiksel özelliklerinin belirlenmesi daha kolaydır.
S: Doğrusal regresyonun bazı pratik kullanımları nelerdir?
C: Doğrusal regresyon, tahminler, öngörüler veya indirgemeler yapmak amacıyla gözlemlenen değerlere (verilere) öngörücü bir model uydurmak için kullanılabilir. Ayrıca değişkenler arasındaki ilişkilerin gücünü ölçmek ve başka bir değişken hakkında gereksiz bilgi içeren veri alt kümelerini tanımlamak için de kullanılabilir.
S: Doğrusal regresyon modelleri hataları nasıl en aza indirmeye çalışır?
C: Doğrusal regresyon modelleri, doğru ile veri noktaları (artıklar) arasındaki dikey mesafeyi mümkün olduğunca küçük yapmaya çalışır. Bu, kalıntıların karelerinin toplamını (en küçük kareler), başka bir normda uyum eksikliğini (en küçük mutlak sapmalar) veya en küçük kareler kayıp fonksiyonunun cezalandırılmış bir versiyonunu (ridge regresyonu) en aza indirerek yapılır.
S: Doğrusal regresyon modellerinin en küçük karelere dayanmaması mümkün müdür?
C: Evet, doğrusal regresyon modellerinin en küçük karelere dayanmaması, bunun yerine başka bir normda uyum eksikliğini en aza indirme (en küçük mutlak sapmalar) veya en küçük kareler kayıp fonksiyonunun cezalandırılmış bir versiyonunu en aza indirme (ridge regresyonu) gibi yöntemleri kullanması mümkündür.
S: "Doğrusal model" ve "en küçük kareler" eşanlamlı mıdır?
C: Hayır, eş anlamlı değildirler. Birbirleriyle yakından bağlantılı olsalar da, "doğrusal model" özellikle düz bir çizgi kullanmayı ifade ederken, "en küçük kareler" özellikle çizgi ile veri noktaları arasında minimum dikey mesafe olmasını sağlayarak hataları en aza indirmeye çalışmayı ifade eder.
Ansiklopedi içinde ara