Birim çemberi
Matematikte birim çember, yarıçapı 1 olan bir çemberdir. Birim çemberin denklemi x 2 + y 2 = 1 {\displaystyle x^{2}+y^{2}=1}
şeklindedir. Birim çember Orijin'de ya da (0,0) koordinatlarında merkezlenir. Trigonometride sıklıkla kullanılır.
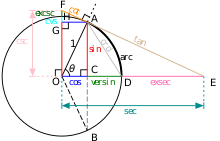
Birim Çember her Trigonometrik fonksiyonu modellemek için kullanılabilir.
Birim çemberde trigonometrik fonksiyonlar
Birim çemberde, t {\displaystyle t}
istenen açı olduğunda, x {\displaystyle x}
ve y {\displaystyle y}
cos ( t ) = x {\displaystyle \cos(t)=x}
ve sin ( t ) = y {\displaystyle \sin(t)=y}
olarak tanımlanabilir. Birim çember fonksiyonunu kullanarak, x 2 + y 2 = 1 {\displaystyle x^{2}+y^{2}=1} birim daire için başka bir denklem bulunur, cos 2 ( t ) + sin 2 ( t ) = 1 {\displaystyle \cos ^{2}(t)+\sin ^{2}(t)=1}
. Trigonometrik fonksiyonlarla çalışırken, ölçüleri 0 ile π 2 {\displaystyle \pi \over 2}
radyan veya 0 ile 90 derece arasında olan açıları kullanmak genellikle yararlıdır. Ancak bundan daha yüksek açılara sahip olmak da mümkündür. Birim çember kullanılarak iki özdeşlik bulunabilir: cos ( t ) = cos ( 2 ⋅ π k + t ) {\displaystyle \cos(t)=\cos(2\cdot \pi k+t)}
ve s i n ( t ) = sin ( 2 ⋅ π k + t ) {\displaystyle sin(t)=\sin(2\cdot \pi k+t)}
herhangi bir k tamsayısı için {\displaystyle k}
.
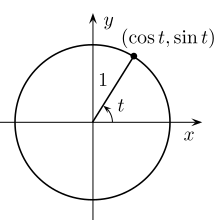
Birim çember, trigonometrik fonksiyonlar için değişkenlerin yerine geçebilir.
Sorular ve Yanıtlar
S: Birim çember nedir?
C: Birim çember, yarıçapı 1 olan bir çemberdir.
S: Birim çemberin denklemi nedir?
C: Birim çemberin denklemi x^2 + y^2 = 1'dir.
S: Birim çemberin merkezi neresidir?
C: Birim çember Orijin'de veya (0,0) koordinatlarında ortalanır.
S: Birim çemberin matematikteki amacı nedir?
C: Birim çember genellikle Trigonometride kullanılır.
S: Birim çember neden önemlidir?
C: Birim çember önemlidir çünkü açılar ve trigonometrik fonksiyonlar arasındaki ilişkilerin anlaşılmasına yardımcı olur.
S: Birim çemberin yarıçapı nedir?
C: Birim çemberin yarıçapı 1'dir.
S: Birim çemberin yarıçapının 1 olmasının önemi nedir?
C: Birim çemberin yarıçapının 1 olmasının önemi, hesaplamaları basitleştirmesi ve açıları trigonometrik değerlerle ilişkilendirmeyi kolaylaştırmasıdır.
