Matematik

Matematik sayıların, şekillerin ve örüntülerin incelenmesidir. Kelime Yunanca "bilim, bilgi veya öğrenme" anlamına gelen "μάθημα" (máthema) kelimesinden gelir ve bazen maths (İngiltere, Avustralya, İrlanda ve Yeni Zelanda'da) veya math (Amerika Birleşik Devletleri ve Kanada'da) olarak kısaltılır. Bu kısa kelimeler genellikle öğrenciler ve okulları tarafından aritmetik, geometri veya basit cebir için kullanılır.

Matematik şu konuları içerir:

Sayılar: şeylerin nasıl sayılabileceği.
Yapı: şeylerin nasıl organize edildiği. Bu alt alan genellikle cebir olarak adlandırılır.
Yer: şeylerin nerede olduğu ve düzenleri. Bu alt alan genellikle geometri olarak adlandırılır.
Değişim: şeylerin nasıl farklı hale geldiği. Bu alt alan genellikle analiz olarak adlandırılır.

Matematik, gerçek dünyada ortaya çıkan sorunları çözmek için yararlıdır, bu nedenle matematikçiler dışında birçok insan matematik çalışır ve kullanır. Günümüzde pek çok işte bir miktar matematiğe ihtiyaç duyulmaktadır. İş dünyasında, bilimde, mühendislikte ve inşaat sektöründe çalışan insanlar matematik bilgisine ihtiyaç duymaktadır.

Matematikte problem çözme

Matematik, problemleri mantık kullanarak çözer. Matematikçiler tarafından kullanılan temel mantık araçlarından biri tümdengelimdir. Tümdengelim, eski doğruları kullanarak yeni doğruları keşfetmek ve kanıtlamak için kullanılan özel bir düşünme biçimidir. Bir matematikçi için, bir şeyin doğru olmasının nedeni (kanıt olarak adlandırılır), doğru olması kadar önemlidir ve bu neden genellikle tümdengelim kullanılarak bulunur. Tümdengelimi kullanmak, matematik düşüncesini deneylere veya görüşmelere dayanan diğer bilimsel düşünme türlerinden farklı kılan şeydir.

Mantık ve akıl yürütme, matematikçiler tarafından matematiğin önemli bir parçası olan genel kurallar oluşturmak için kullanılır. Bu kurallar önemli olmayan bilgileri dışarıda bırakır, böylece tek bir kural birçok durumu kapsayabilir. Genel kurallar bularak matematik birçok problemi aynı anda çözer, çünkü bu kurallar başka problemlerde de kullanılabilir. Bu kurallar teorem (kanıtlanmışlarsa) veya varsayım (henüz doğru olup olmadıkları bilinmiyorsa) olarak adlandırılabilir. Çoğu matematikçi mantıksal bir kanıt bulmak için mantıksal olmayan ve yaratıcı akıl yürütmeler kullanır.

Bazen matematik, henüz anlamadığımız kuralları veya fikirleri bulur ve inceler. Matematikte genellikle fikirler ve kurallar basit ya da düzgün oldukları düşünüldüğü için seçilir. Öte yandan, bazen bu fikirler ve kurallar matematikte çalışıldıktan sonra gerçek dünyada bulunur; bu geçmişte birçok kez olmuştur. Genel olarak, matematiğin kurallarını ve fikirlerini çalışmak dünyayı daha iyi anlamamıza yardımcı olabilir. Matematik problemlerine örnek olarak toplama, çıkarma, çarpma, bölme, kalkülüs, kesirler ve ondalık sayılar verilebilir. Cebir problemleri belirli değişkenler değerlendirilerek çözülür. Bir hesap makinesi, dört temel aritmetik işlemdeki her matematik problemini yanıtlar.

Matematikte çalışma alanları

Sayı

Matematik, sayıların ve miktarların incelenmesini içerir ve şekil, miktar ve düzenleme mantığı ile ilgilenen bir bilim dalıdır. Aşağıda listelenen alanların çoğu, küme teorisi ve matematiksel mantık da dahil olmak üzere matematiğin birçok farklı alanında çalışılmaktadır. Sayı teorisi çalışması genellikle sayıların gerçek temellerinden ziyade tam sayıların yapısı ve davranışına odaklanır ve bu nedenle bu alt bölümde listelenmemiştir.

0 , 1 , 2 , 3 , ... {\displaystyle 0,1,2,3,\ldots } $0,1,2,3,\ldots$	... , - 1 , 0 , 1 , ... {\displaystyle \ldots ,-1,0,1,\ldots } $\ldots ,-1,0,1,\ldots$	1 2 , 2 3 , 0.125 , ... {\displaystyle {\frac {1}{2}},{\frac {2}{3}},0.125,\ldots } ${\frac {1}{2}},{\frac {2}{3}},0.125,\ldots$	π , e , 2 , ... {\displaystyle \pi ,e,{\sqrt {2}},\ldots } $\pi ,e,{\sqrt {2}},\ldots$	1 + i , 2 e i π / 3 , ... {\displaystyle 1+i,2e^{i\pi /3},\ldots } $1+i,2e^{i\pi /3},\ldots$
Doğal sayılar	Tamsayılar	Rasyonel sayılar	Gerçek sayılar	Karmaşık sayılar
0 , 1 , ... , ω , ω + 1 , ... , 2 ω , ... {\displaystyle 0,1,\ldots ,\omega ,\omega +1,\ldots ,2\omega ,\ldots } $0,1,\ldots ,\omega ,\omega +1,\ldots ,2\omega ,\ldots$	ℵ 0 , ℵ 1 , ... {\displaystyle \aleph _{0},\aleph _{1},\ldots } $\aleph _{0},\aleph _{1},\ldots$	+ , - , × , ÷ {\displaystyle +,-,\times ,\div } $+,-,\times ,\div$	> , ≥ , = , ≤ , < {\displaystyle >,\geq ,=,\leq ,< } $>,\geq ,=,\leq ,<$	f ( x ) = x {\displaystyle f(x)={\sqrt {x}} $f(x)={\sqrt {x}}$
Sıralı sayılar	Kardinal sayılar	Aritmetik işlemler	Aritmetik ilişkiler	Fonksiyonlar

Yapı

Matematiğin birçok alanı bir nesnenin sahip olduğu yapıyı inceler. Bu alanların çoğu cebir çalışmasının bir parçasıdır.


Sayı teorisi	Soyut cebir	Doğrusal cebir	Düzen teorisi	Çizge teorisi

Şekil

Matematiğin bazı alanları nesnelerin şekillerini inceler. Bu alanların çoğu geometri çalışmasının bir parçasıdır.


Topoloji	Geometri	Trigonometri	Diferansiyel geometri	Fraktal geometri

Değişim

Matematiğin bazı alanları nesnelerin nasıl değiştiğini inceler. Bu alanların çoğu analiz çalışmasının bir parçasıdır.


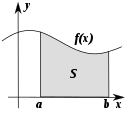
Kalkülüs	Vektör hesabı	Analiz

Diferansiyel denklemler	Dinamik sistemler	Kaos teorisi

Uygulamalı matematik

Uygulamalı matematik, mühendislik, fizik ve bilgisayar gibi diğer alanlardaki problemleri çözmek için matematiği kullanır.

Sayısal analiz - Optimizasyon - Olasılık teorisi - İstatistik - Matematiksel finans - Oyun teorisi - Matematiksel fizik - Akışkanlar dinamiği - Hesaplamalı algoritmalar

Ünlü teoremler

Bu teoremler matematikçilerin ve matematikçi olmayan insanların ilgisini çekmiştir.

Pisagor teoremi - Fermat'ın son teoremi - Goldbach varsayımı - İkiz Asal Varsayımı - Gödel'in eksiklik teoremleri - Poincaré varsayımı - Cantor'un köşegen argümanı - Dört renk teoremi - Zorn'un lemması - Euler Özdeşliği - Church-Turing tezi

Bunlar matematiği büyük ölçüde değiştiren teoremler ve varsayımlardır.

Riemann hipotezi - Süreklilik hipotezi - P Versus NP - Pisagor teoremi - Merkezi limit teoremi - Kalkülüsün temel teoremi - Cebirin temel teoremi - Aritmetiğin temel teoremi - Projektif geometrinin temel teoremi - Yüzeylerin sınıflandırma teoremleri - Gauss-Bonnet teoremi - Fermat'ın son teoremi - Kantorovich teoremi

Temeller ve yöntemler

Matematiğin doğasını anlamadaki ilerleme, matematikçilerin konularını çalışma biçimlerini de etkilemektedir.

Matematik Felsefesi - Matematiksel sezgicilik - Matematiksel yapılandırmacılık - Matematiğin temelleri - Küme teorisi - Sembolik mantık - Model teorisi - Kategori teorisi - Mantık - Tersine Matematik - Matematiksel semboller tablosu

Tarih ve matematikçilerin dünyası

Tarihte matematik ve matematiğin tarihi.

Matematik tarihi - Matematiğin zaman çizelgesi - Matematikçiler - Fields madalyası - Abel Ödülü - Milenyum Ödülü Problemleri (Clay Math Prize) - Uluslararası Matematik Birliği - Matematik yarışmaları - Yanal düşünme - Matematik ve cinsiyet

Matematik alanında ödüller

Matematikte Nobel ödülü yoktur. Matematikçiler önemli çalışmaları için Abel ödülü ve Fields Madalyası alabilirler.

Clay Matematik Enstitüsü, Milenyum Ödülü Problemlerinden birini çözen kişiye bir milyon dolar vereceğini açıkladı.

Matematiksel araçlar

Matematik yapmak veya matematik problemlerine cevap bulmak için kullanılan birçok araç vardır.

Eski araçlar

Abaküs
Napier'in kemikleri, sürgülü cetvel
Cetvel ve Pusula
Zihinsel hesaplama

Daha yeni araçlar

Hesap makineleri ve bilgisayarlar
Programlama dilleri
Bilgisayar cebir sistemleri (listeleme)
İnternet steno gösterimi
istatistiksel analiz yazılımı (örneğin SPSS)
SAS programlama dili
R programlama dili

Ayrıca Bakınız

Matematikte kadınların zaman çizelgesi
Amerikan Matematik Derneği
Endüstriyel ve Uygulamalı Matematik Derneği
Matematik Soyağacı Projesi
Matematik Konu Sınıflandırması

Sorular ve Yanıtlar

S: Matematik nedir?

C: Matematik sayıların, şekillerin ve örüntülerin incelenmesidir. Kelime Yunanca μάθημα (máthema) kelimesinden gelmektedir ve "bilim, bilgi veya öğrenme" anlamına gelmektedir.

S: Matematiğin temel alanları nelerdir?

C: Matematiğin ana alanları sayılar, yapı (cebir), yer (geometri) ve değişimdir (analiz).

S: Matematik gerçek dünyada nasıl kullanılır?

C: Uygulamalı matematik, gerçek dünya problemlerini çözmek için faydalıdır. İş, bilim, mühendislik ve inşaat alanlarında çalışan kişiler matematiği kullanır.

S: "Matematik" kelimesinin kısaltılmış bir versiyonu var mı?

C: Evet - İngiliz Milletler Topluluğu ülkelerinde "maths" veya Kuzey Amerika'da "math" olarak kısaltılabilir.

S: 'Matematik' kelimesi ne anlama geliyor?

C: 'Matematik' kelimesi Yunanca μάθημα (máthema) kelimesinden gelmektedir ve 'bilim, bilgi veya öğrenme' anlamına gelmektedir.

S: Uygulamalı matematik ne tür problem çözmeyi içerir?

C: Uygulamalı matematik, iş, bilim, mühendislik ve inşaat alanlarında çalışan kişilerin karşılaştığı gerçek dünya problemlerini çözmeyi içerir.