Slayt kuralı

Temel kavramlar

En temel haliyle sürgülü cetvel, sayıların hızlı bir şekilde çarpılmasını ve bölünmesini sağlamak için iki logaritmik ölçek kullanır. Bu yaygın işlemler kağıt üzerinde yapıldığında zaman alıcı ve hataya açık olabilir. Daha karmaşık sürgülü cetveller karekök, üstel, logaritma ve trigonometrik fonksiyonlar gibi diğer hesaplamalara olanak sağlar.

Matematiksel hesaplamalar, kayan merkezi şerit üzerindeki bir işaretin sabit şeritlerden biriyle hizalanmasıyla yapılır. Daha sonra diğer işaretlerin göreceli konumu gözlemlenebilir. İşaretlerle hizalanan sayılar çarpımın, bölümün veya hesaplanan diğer sonucun yaklaşık değerini verir.

Kullanıcı, zihinsel tahmine dayalı olarak sonuçtaki ondalık noktanın yerini belirler. Bilimsel gösterim, daha resmi hesaplamalarda ondalık noktayı izlemek için kullanılır. Bir hesaplamadaki toplama ve çıkarma adımları genellikle sürgülü cetvel üzerinde değil, zihinsel olarak veya kağıt üzerinde yapılır.

Çoğu sürgülü cetvelde aynı uzunlukta üç doğrusal şerit bulunur. Şeritler paralel olarak hizalanır ve birbirine kenetlenir, böylece merkezi şerit diğer ikisine göre uzunlamasına hareket ettirilebilir. Dıştaki iki şerit, göreceli konumları değişmeyecek şekilde sabitlenmiştir.

Bazı sürgülü cetvellerde ("dubleks" modeller) cetvelin ve sürgü şeridinin her iki tarafında, diğerlerinde dış şeritlerin bir tarafında ve sürgü şeridinin her iki tarafında, diğerlerinde ise sadece bir tarafta ölçekler bulunur ("simpleks" cetveller). Dikey hizalama çizgisine sahip kayan bir imleç, yan yana olmayan veya dubleks modellerde cetvelin diğer tarafında bulunan ölçeklerdeki karşılık gelen noktaları bulmak için kullanılır. İmleç ayrıca ölçeklerden herhangi birinde bir ara sonuç kaydedebilir.

Sürgülü cetvel üzerinde imleç

Hesaplama için sürgülü cetvel kullanma

Çarpma İşlemi

Bir logaritma, log ( x y ) = log ( x ) + log ( y ) {\displaystyle \log(xy)=\log(x)+\log(y)} ve log ( x / y ) = log ( x ) - log ( y ) {\displaystyle \log(x/y)=\log(x)-\log(y)} kurallarına göre çarpma ve bölme işlemlerini toplama ve çıkarmaya dönüştürür. Üst ölçeği log ( x ) {\displaystyle \log(x)} kadar sağa kaydırarak, üst ölçeğin başlangıcını alttaki x {\displaystyle x} etiketiyle eşleştirerek, her y {\displaystyle y} sayısını hizalar. log ( y ) {\displaystyle \log(y)} konumunda üst ölçekte, log ( x ) + log ( y ) {\displaystyle \log(x)+\log(y)} konumundaki sayı ise alt ölçekte yer almaktadır. log ( x ) + log ( y ) = log ( x y ) {\displaystyle \log(x)+\log(y)=\log(xy)} olduğundan, alt ölçekteki bu konum x y {\displaystyle xy} sayısını verir. x {\displaystyle x} ve y {\displaystyle y} çarpımıdır. Örneğin, 3*2'yi hesaplamak için üst ölçekteki 1, alt ölçekteki 2'ye taşınır. Cevap olan 6, 3'ün üst ölçekte olduğu alt ölçekten okunur. Genel olarak, üstteki 1 alttaki bir faktöre taşınır ve cevap, diğer faktörün üstte olduğu yerde alttan okunur.

İşlemler "ölçek dışına" çıkabilir; örneğin, yukarıdaki şemada sürgülü cetvelin üst ölçekteki 7'yi alt ölçekteki herhangi bir sayının üzerine konumlandırmadığı görülmektedir, bu nedenle 2×7 için herhangi bir yanıt vermez. Bu gibi durumlarda, kullanıcı üst ölçeği sağ indeksi 2 ile aynı hizaya gelene kadar sola kaydırabilir ve aşağıdaki resimde olduğu gibi 2 yerine 0,2 ile çarpabilir:

Burada sürgülü cetvel kullanıcısı, nihai cevabı düzeltmek için ondalık noktayı uygun şekilde ayarlamayı unutmamalıdır. 2×7'yi bulmak istedik, ancak bunun yerine 0,2×7=1,4 olarak hesapladık. Yani gerçek cevap 1,4 değil 14'tür. Sürgüyü sıfırlamak, 2×7 gibi ölçek dışı sonuçlara neden olabilecek çarpma işlemlerini gerçekleştirmenin tek yolu değildir; başka bazı yöntemler de vardır:

• (1) A ve B çift onlu ölçeklerini kullanın.
• (2) Katlanmış terazileri kullanın. Bu örnekte, C'nin sol 1'ini D'nin 2'sinin karşısına ayarlayın. İmleci CF'de 7'ye getirin ve sonucu DF'den okuyun.
• (3) Ters çevrilmiş CI ölçeğini kullanın. CI ölçeğindeki 7'yi D ölçeğindeki 2'nin üzerine yerleştirin ve ardından sonucu D ölçeğinden, CI ölçeğindeki 1'in altından okuyun. CI ölçeğinde 1 iki yerde bulunduğundan, bunlardan biri her zaman ölçek üzerinde olacaktır.
• (4) Hem CI ters skalasını hem de C skalasını kullanın. CI'nın 2'sini D'nin 1'i ile hizalayın ve sonucu D'den, C skalasındaki 7'nin altından okuyun.

Yöntem 1'in anlaşılması kolaydır, ancak hassasiyet kaybına neden olur. Yöntem 3, yalnızca iki ölçek içermesi avantajına sahiptir.

Bölüm

Aşağıdaki resim 5,5/2'nin hesaplanmasını göstermektedir. Üst ölçekteki 2, alt ölçekteki 5,5'in üzerine yerleştirilmiştir. Üst ölçekteki 1, bölüm olan 2,75'in üzerinde yer alır. Bölme işlemi için birden fazla yöntem vardır, ancak burada sunulan yöntemin avantajı, nihai sonucun ölçek dışı olmamasıdır, çünkü her iki uçta da 1'i kullanma seçeneği vardır.

Diğer operasyonlar

Logaritmik ölçeklere ek olarak, bazı sürgülü cetvellerde diğer yardımcı ölçekler üzerinde kodlanmış başka matematiksel işlevler de bulunmaktadır. En popüler olanları trigonometrik, genellikle sinüs ve tanjant, ortak logaritma (log10) (bir çarpan ölçeğinde bir değerin logunu almak için), doğal logaritma (ln) ve üstel (e^x ) ölçeklerdir. Bazı kurallar, üçgenlerin kenarlarını bulmak için Pisagor ölçeğini ve daireleri bulmak için bir ölçeği içerir. Diğerleri hiperbolik fonksiyonları hesaplamak için ölçekler içerir. Doğrusal kurallarda, ölçekler ve bunların etiketlenmesi oldukça standartlaştırılmıştır ve genellikle yalnızca hangi ölçeklerin dahil edildiği ve hangi sırada olduğu konusunda farklılıklar meydana gelir:

A, B	sayıların kareköklerini ve karelerini bulmak için kullanılan iki ondalık logaritmik ölçekler
C, D	tek on yıllık logaritmik ölçekler
K	sayıların küp köklerini ve küplerini bulmak için kullanılan üç onlu logaritmik ölçek
CF, DF	C ve D skalalarının birlik yerine π'den başlayan "katlanmış" versiyonları; bunlar iki durumda kullanışlıdır. İlk olarak, kullanıcı bir ürünün 10'a yakın olacağını tahmin ettiğinde ancak 10'dan biraz daha az mı yoksa biraz daha fazla mı olacağından emin olmadığında, katlanmış ölçekler ölçeğin dışına çıkma olasılığını önler. İkincisi, başlangıcı 10'un karekökü yerine π yaparak, π ile çarpma veya bölme (fen ve mühendislik formüllerinde yaygın olduğu gibi) basitleştirilmiştir.
CI, DI, DIF	1/x adımlarını basitleştirmek için kullanılan, sağdan sola doğru ilerleyen "ters" ölçekler
S	D ölçeğinde sinüs ve kosinüsleri bulmak için kullanılır
T	D ve DI ölçeklerinde teğet ve kotanjantları bulmak için kullanılır
ST, SRT	küçük açıların sinüs ve tanjantları ve derece-radyan dönüşümü için kullanılır
L	10'un tabanı logaritmaları ve 10'un kuvvetlerini bulmak için C ve D ölçekleriyle birlikte kullanılan doğrusal bir ölçek
LLn	sayıların logaritmalarını ve üstellerini bulmak için kullanılan bir log-log ölçekler kümesi
Ln	doğal (e tabanı) logaritmaları ve e x {\displaystyle e^{x}} bulmak için C ve D ölçekleriyle birlikte kullanılan doğrusal bir ölçektir.

 

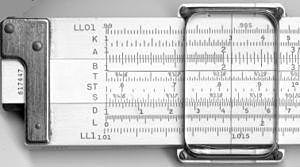
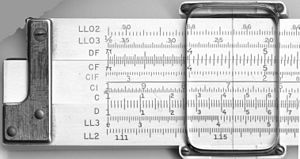
Bir K&E 4081-3 sürgülü cetvelin ön ve arka tarafındaki ölçekler.

Gilson tarafından 1931 yılında üretilen İkili Kaydırmalı Cetvel, kesirlerle sınırlı bir toplama ve çıkarma işlevi gerçekleştiriyordu.

Kökler ve güçler

Tek onlu (C ve D), çift onlu (A ve B) ve üç onlu (K) ölçekler vardır. x 2'yi hesaplamak için {\displaystyle x^{2}} Örneğin, D ölçeğinde x'i bulun ve A ölçeğinde karesini okuyun. Bu işlemin tersine çevrilmesi kareköklerin bulunmasını sağlar ve benzer şekilde 3, 1/3, 2/3 ve 3/2 kuvvetleri için de geçerlidir. Taban, x, ölçeğinde birden fazla yerde bulunduğunda dikkatli olunmalıdır. Örneğin, A ölçeğinde iki dokuz vardır; dokuzun karekökünü bulmak için birincisini kullanın; ikincisi 90'ın karekökünü verir.

x y {\displaystyle x^{y}} problemleri için LL ölçeklerini kullanın. Birden fazla LL ölçeği mevcutsa, üzerinde x olan ölçeği kullanın. İlk olarak, C ölçeğindeki en soldaki 1'i LL ölçeğindeki x ile hizalayın. Ardından, C ölçeğinde y'yi bulun ve üzerinde x olan LL ölçeğine gidin. Bu ölçek cevabı gösterecektir. Eğer y "ölçek dışındaysa", x y / 2 {\displaystyle x^{y/2}} bulun ve yukarıda açıklandığı gibi A ve B ölçeklerini kullanarak karesini alın.

Trigonometri

S, T ve ST ölçekleri, derece cinsinden açılar için trigonometrik fonksiyonlar ve trigonometrik fonksiyonların katları için kullanılır. Birçok sürgülü cetvelin S, T ve ST ölçekleri derece ve dakika ile işaretlenmiştir. Decitrig olarak adlandırılan modeller bunun yerine derecelerin ondalık kesirlerini kullanır.

Logaritma ve üstel sayılar

10 tabanı logaritmaları ve üstelleri, doğrusal olan L ölçeği kullanılarak bulunur. Bazı sürgülü cetvellerde e tabanı için Ln ölçeği vardır.

Ln ölçeği 1958 yılında 11. sınıf öğrencisi Stephen B. Cohen tarafından icat edilmiştir. Orijinal amaç, kullanıcının Ln ölçeğinde bir x üssü (0 ila 2,3 aralığında) seçmesine ve C (veya D) ölçeğinde e^x ve CI (veya DI) ölçeğinde e^–x okumasına izin vermekti. Pickett, Inc. şirketine ölçeğin münhasır hakları verilmiştir. Daha sonra, mucit Ln ölçeğinde aralığı 2,3 sınırının ötesine genişletmek için bir dizi "işaret" oluşturdu, ancak Pickett bu işaretleri hiçbir zaman sürgülü cetvellerine dahil etmedi. ^[]

Toplama ve çıkarma

Kaydırma kuralları genellikle toplama ve çıkarma işlemleri için kullanılmaz, ancak yine de iki farklı teknik kullanarak bunu yapmak mümkündür.

C ve D (veya benzer ölçekler) üzerinde toplama ve çıkarma yapmak için ilk yöntem, problemi bölme işlemine dönüştürmeyi gerektirir. Toplama işlemi için, iki değişkenin bölümü artı bölenin bir katı toplamlarına eşittir:

x + y = ( x y + 1 ) y {\displaystyle x+y=\left({\frac {x}{y}}+1\right)y}

Çıkarma işlemi için, iki değişkenin bölümü eksi bölenin bir katı, bunların farkına eşittir:

x - y = ( x y - 1 ) y {\displaystyle x-y=\left({\frac {x}{y}}-1\right)y}

Bu yöntem, Gravity Pipe (GRAPE) süper bilgisayarı ve gizli Markov modelleri gibi özel bilgisayar uygulamalarında logaritmik sayı sistemi ile yüksek hızlı elektronik devreler için kullanılan toplama/çıkarma tekniğine benzer.

İkinci yöntem, bazı modellerde bulunan kayan bir doğrusal L ölçeği kullanır. Toplama ve çıkarma, imleç sola (çıkarma için) veya sağa (toplama için) kaydırılarak ve ardından sonucu okumak için kaydırma 0'a döndürülerek gerçekleştirilir.

Fiziksel tasarım

Standart doğrusal kurallar

Sürgülü cetvelin uzunluğu, ölçeklerin nominal uzunluğu cinsinden belirtilir. En yaygın "10 inç" modellerindeki ölçekler, metrik standartlara göre yapıldıkları için aslında 25 cm uzunluğundadır, ancak bazı kurallar, bir sonuç taştığında manipülasyonu basitleştirmek için biraz uzatılmış ölçekler sunar. Cep cetvelleri tipik olarak 5 inçtir. Birkaç metre uzunluğundaki modeller, öğretim amacıyla sınıflara asılmak üzere satılmıştır. [1]

Tipik olarak bölümler bir ölçeği iki anlamlı rakam hassasiyetinde işaretler ve kullanıcı üçüncü rakamı tahmin eder. Bazı üst düzey sürgülü cetvellerde, işaretlerin görülmesini kolaylaştıran büyüteçler bulunur. Bu tür imleçler, okumaların doğruluğunu etkili bir şekilde iki katına çıkarabilir ve 10 inçlik bir sürgülü cetvelin 20 inçlik bir cetvel kadar iyi hizmet vermesine izin verir.

Çeşitli başka kolaylıklar da geliştirilmiştir. Trigonometrik ölçekler bazen "Darmstadt" tarzı olarak adlandırılan tamamlayıcı açılarla siyah ve kırmızı olarak çift etiketlenir. Çift taraflı sürgülü cetveller genellikle arkadaki bazı ölçekleri çoğaltır. Daha yüksek doğruluk elde etmek için ölçekler genellikle "bölünür".

Çeşitli mühendislik, işletme ve bankacılık türleri için özel sürgülü cetveller icat edildi. Bunlar genellikle kredi hesaplamaları, optimum satın alma miktarları veya belirli mühendislik denklemleri gibi doğrudan özel ölçekler olarak ifade edilen ortak hesaplamalara sahipti. Örneğin Fisher Controls şirketi, endüstriyel akış kontrol valflerinin uygun boyutunu seçmek için kullanılan denklemleri çözmeye uyarlanmış özelleştirilmiş bir sürgülü cetvel dağıtmıştır. ^[]

Dairesel sürgülü cetveller

Dairesel sürgülü cetveller, biri iki imleçli (solda) ve diğeri hareketli bir disk ve tek bir imleçli (sağda) olmak üzere iki temel tipte gelir. Çift imleçli versiyonlar, kadran etrafında döndürülürken imleçler arasında sabit bir açıyı koruyarak çarpma ve bölme işlemlerini gerçekleştirir. Tek imleçli versiyon, ölçeklerin uygun şekilde hizalanması sayesinde daha çok standart sürgülü cetvel gibi çalışır.

Dairesel bir sürgülü cetvelin temel avantajı, aletin en uzun boyutunun yaklaşık 3 kat (yani π kadar) azaltılmış olmasıdır. Örneğin, 10 cm'lik bir daireselin dış ölçeği, 30 cm'lik sıradan bir sürgülü cetvele eşit bir maksimum hassasiyete sahip olacaktır. Dairesel sürgülü cetveller "ölçek dışı" hesaplamaları da ortadan kaldırır, çünkü ölçekler "etrafı saracak" şekilde tasarlanmıştır; sonuçlar 1.0'a yaklaştığında asla yeniden yönlendirilmeleri gerekmez - cetvel her zaman ölçektedir. Bununla birlikte, S, T ve LL'ler gibi döngüsel olmayan spiral olmayan ölçeklerde, uç kenar boşluklarına yer açmak için ölçek uzunluğu kısaltılır.

Dairesel sürgülü cetveller mekanik olarak daha sağlamdır ve daha yumuşak hareket eder, ancak ölçek hizalama hassasiyeti merkezi bir pivotun merkezlenmesine duyarlıdır; pivotun 0,1 mm'lik bir merkezden uzaklığı, en kötü durumda 0,2 mm'lik bir hizalama hatasına neden olabilir. Bununla birlikte pivot, yüzün ve imleçlerin çizilmesini önler. En yüksek hassasiyete sahip ölçekler dış halkalara yerleştirilmiştir. "Bölünmüş" teraziler yerine, üst düzey dairesel kurallar log-of-log terazileri gibi daha karmaşık işlemler için spiral teraziler kullanır. Sekiz inçlik birinci sınıf bir dairesel cetvelde 50 inçlik bir spiral log-log ölçeği vardı.

Dairesel sürgülü cetvellerin ana dezavantajları, dönen bir disk boyunca şekillerin yerini belirlemenin zorluğu ve sınırlı sayıda ölçektir. Dairesel sürgülü cetvellerin bir diğer dezavantajı da daha az önemli ölçeklerin merkeze daha yakın olması ve daha düşük hassasiyete sahip olmasıdır. Çoğu öğrenci sürgülü cetvel kullanımını doğrusal sürgülü cetvellerde öğrenmiş ve değiştirmek için bir neden bulamamıştır.

Dünya çapında günlük kullanımda kalan bir sürgülü cetvel E6B'dir. Bu, ilk olarak 1930'larda uçak pilotlarının ölü hesaplamaya yardımcı olması için yaratılmış dairesel bir sürgülü cetveldir. Çerçeve üzerine basılmış ölçekler yardımıyla zaman, mesafe, hız ve sıcaklık değerlerini dönüştürme, pusula hataları ve yakıt kullanımını hesaplama gibi çeşitli görevlere de yardımcı olur. "Dua çarkı" olarak adlandırılan bu alet halen uçuş mağazalarında bulunmakta ve yaygın olarak kullanılmaktadır. GPS havadan seyrüsefer için ölü hesap kullanımını azaltmış ve el tipi hesap makineleri birçok işlevini devralmış olsa da, E6B birincil veya yedek cihaz olarak yaygın şekilde kullanılmaya devam etmektedir ve uçuş okullarının çoğu öğrencilerinin bir dereceye kadar ustalaşmasını talep etmektedir.

İsviçreli saat şirketi Breitling, 1952 yılında uçuş hesaplamaları için özel olarak tasarlanmış entegre dairesel sürgülü cetvele sahip bir pilot kol saati tanıttı: Breitling Navitimer. Breitling tarafından "navigasyon bilgisayarı" olarak adlandırılan Navitimer dairesel cetvel, hava hızı, tırmanma/iniş hızı/zamanı, uçuş süresi, mesafe ve yakıt tüketimi işlevlerinin yanı sıra kilometre-nötr mil ve galon-litre yakıt miktarı dönüştürme işlevlerine sahipti.

Malzemeler

Geleneksel olarak sürgülü cetveller maun veya şimşir ağacı gibi sert ahşaptan yapılır ve imleçleri cam ve metalden olurdu. En az bir yüksek hassasiyetli alet çelikten yapılmıştır.

1895 yılında Hemmi adlı bir Japon firması, boyutsal olarak kararlı, güçlü ve doğal olarak kendi kendini yağlama avantajlarına sahip olan bambudan sürgülü cetveller yapmaya başladı. Bu bambu sürgülü cetveller Eylül 1933'te İsveç'te [2] ve muhtemelen biraz daha erken bir tarihte Almanya'da tanıtıldı. Ölçekler selüloit veya plastikten yapılmıştı. Daha sonraki sürgülü cetveller plastikten ya da plastikle boyanmış alüminyumdan yapılmıştır. Daha sonraki imleçler teflon yataklar üzerinde kayan akrilik veya polikarbonattı.

Tüm birinci sınıf sürgülü cetvellerde sayılar ve ölçekler kazınmış ve ardından boya veya başka bir reçine ile doldurulmuştur. Boyalı veya baskılı sürgülü cetveller, işaretler aşınabildiği için daha düşük kaliteli olarak görülüyordu. Bununla birlikte, muhtemelen Amerika'nın en başarılı sürgülü cetvel şirketi olan Pickett, tüm baskılı ölçekleri üretti. Birinci sınıf sürgülü cetvellerde, cetvelin kazara düşmemesi için akıllı mandallar ve terazi ile imleci masaüstüne sürtünmekten korumak için tamponlar bulunurdu. Kazınmış işaretler için önerilen temizleme yöntemi çelik yünü ile hafifçe ovmaktır. Boyalı cetveller içinse seyreltilmiş ticari cam temizleme sıvısı ve yumuşak bir bez kullanın.

İki imleçli Pickett dairesel sürgülü cetvel. (4,25 inç / 10,9 cm çapında) Arka yüzünde ek ölçek ve bir imleç vardır.


Concise Co., Ltd., Tokyo, Japonya tarafından yapılmış, sadece ters, kare ve kübik ölçeklere sahip basit bir dairesel sürgülü cetvel. Arka yüzünde 38 metrik/imperial dönüşüm faktörünün kullanışlı bir listesi bulunmaktadır.


Dairesel sürgülü cetvelli Breitling Navitimer kol saati

Tarih

Sürgülü cetvel, John Napier'in logaritma kavramını yayınlamasından kısa bir süre sonra, 1620-1630 yılları arasında icat edilmiştir. Oxford'lu Edmund Gunter, ek ölçüm araçlarıyla çarpma ve bölme işlemlerinde kullanılabilen tek bir logaritmik ölçeğe sahip bir hesaplama cihazı geliştirdi. Bu ölçeğin ilk tanımı 1624 yılında Paris'te İngiliz matematikçi Edmund Wingate (yaklaşık 1593 - 1656) tarafından "L'usage de la reigle de proportion en l'arithmetique & geometrie" başlıklı bir kitapta yayınlanmıştır. Kitap, bir yüzünde logaritmik ölçek, diğer yüzünde ise tablosal ölçek bulunan ikili bir ölçek içermektedir. 1630'da Cambridge'li William Oughtred dairesel bir sürgülü cetvel icat etti ve 1632'de iki Gunter cetvelini elleriyle bir arada tutarak modern sürgülü cetvel olarak bilinen cihazı yaptı. Cambridge'deki çağdaşı Isaac Newton gibi Oughtred de fikirlerini öğrencilerine özel olarak öğretti, ancak yayınlamakta gecikti ve Newton gibi, bir zamanlar öğrencisi olan Richard Delamain ve Wingate'in önceki iddiaları ile öncelik konusunda ateşli bir tartışmaya dahil oldu. Oughtred'in fikirleri ancak öğrencisi William Forster'ın 1632 ve 1653 yıllarındaki yayınlarıyla kamuoyuna duyurulmuştur.

1677 yılında Henry Coggeshall, kereste ölçümü için Coggeshall sürgülü cetveli adı verilen iki ayaklı katlanır bir cetvel yarattı. Bu aletin tasarımı ve kullanımı, sürgülü cetvele matematiksel sorgulamanın dışında bir amaç kazandırdı.

1722'de Warner iki ve üç on yıllık ölçekleri tanıttı ve 1755'te Everard ters çevrilmiş bir ölçek ekledi; tüm bu ölçekleri içeren bir sürgülü cetvel genellikle "çok fazlı" bir cetvel olarak bilinir.

1815 yılında Peter Roget, logaritmanın logaritmasını gösteren bir ölçek içeren log log sürgülü cetveli icat etti. Bu, kullanıcının kökleri ve üsleri içeren hesaplamaları doğrudan yapabilmesini sağladı. Bu özellikle kesirli kuvvetler için kullanışlıydı.

Modern form

Daha modern form 1859'da Fransız topçu teğmeni Amédée Mannheim tarafından yaratılmıştır; Mannheim "kuralını ulusal üne sahip bir firmaya yaptırdığı ve Fransız Topçusu tarafından benimsendiği için şanslıydı." Mühendisliğin tanınan bir mesleki faaliyet haline gelmesiyle birlikte, sürgülü cetveller Avrupa'da yaygın olarak kullanılmaya başlandı. Edwin Thacher'in silindirik bir cetveli tanıttığı 1881 yılına kadar Amerika Birleşik Devletleri'nde yaygınlaşmadılar. Dubleks cetvel 1891 yılında William Cox tarafından icat edilmiş ve New York'ta Keuffel and Esser Co. tarafından üretilmiştir.

Astronomi çalışmaları da ince hesaplamalar gerektiriyordu ve 19. yüzyıl Almanya'sında bir gözlemevinde yaklaşık 2 metre uzunluğunda çelik bir sürgülü cetvel kullanılıyordu. Üzerinde altı ondalık basamağa kadar doğruluk sağlayan bir mikroskop vardı.

Dünya Savaşı'nda, hızlı hesaplamalara ihtiyaç duyan bombardıman pilotları ve navigatörler genellikle özel sürgülü cetveller kullandılar. ABD Donanması'nın bir ofisi, özel hesaplamalar için selüloit kartların (her iki yüzüne de basılmış) yerleştirilebileceği alüminyum gövdeli ve plastik imleçli genel bir sürgülü cetvel "şasisi" tasarladı. Bu işlem uçakların menzilini, yakıt kullanımını ve irtifasını hesaplamak için icat edilmiş ve daha sonra birçok başka amaca uyarlanmıştır.

1950'ler ve 1960'lar boyunca sürgülü cetvel mühendislik mesleğinin sembolü olmuştur (tıpkı stetoskopun tıp mesleğini sembolize etmesi gibi).^[] Alman roket bilimci Wernher von Braun, İkinci Dünya Savaşı'ndan sonra Amerikan uzay programında çalışmak üzere ABD'ye taşındığında yanında iki adet 1930'lardan kalma Nestler sürgülü cetvel getirmişti. Hayatı boyunca başka hiçbir cep hesaplama cihazı kullanmadı; sürgülü cetveller ona roket tasarım parametreleri ve diğer rakamlar hakkında hızlı tahminler yapmak için mükemmel bir şekilde hizmet etti. Pickett'in N600 sürgülü cetvel kutuları üzerindeki reklamlara göre, alüminyum Pickett marka sürgülü cetveller Ay da dahil olmak üzere beş Apollo uzay görevinde taşınmıştır [3].

Bazı mühendislik öğrencileri ve mühendisler kemer kılıflarında on inçlik sürgülü cetveller taşıyordu ve 1970'lerin ortalarında bile bu kampüslerde yaygın bir manzaraydı. Öğrenciler ayrıca evde ya da ofiste hassas çalışmalar için on ya da yirmi inçlik bir cetvel bulundururken yanlarında beş inçlik bir cep sürgülü cetvel de taşıyabiliyordu.

2004 yılında eğitim araştırmacıları David B. Sher ve Dean C. Nataro, logaritmadan önce gelen hızlı çarpım hesaplama algoritması olan prosthaphaeresis'e dayalı yeni bir sürgülü cetvel türü tasarladılar. Bununla birlikte, ilk prototipin ötesinde bir tane inşa etmeye yönelik pratik ilgi çok az olmuştur. [4]

Düşüş

Sürgülü cetvelin önemi, 1950'lerde yeni ama çok kıt bir kaynak olan elektronik bilgisayarların 1960'larda teknik çalışanlar için yaygın olarak kullanılabilir hale gelmesiyle azalmaya başladı. Fortran'ın 1957'de piyasaya sürülmesi, bilgisayarları mütevazı boyuttaki matematik problemlerini çözmek için pratik hale getirdi. IBM, bilim ve mühendislik pazarına yönelik olarak IBM 650 (1954), IBM 1620 (1959), IBM 1130 (1965) gibi bir dizi daha uygun fiyatlı bilgisayar tanıttı. John Kemeny'nin BASIC programlama dili (1964) öğrencilerin bilgisayar kullanmasını kolaylaştırdı. DEC PDP-8 mini bilgisayar 1965 yılında tanıtıldı.

Bilgisayarlar hesaplamanın doğasını da değiştirdi. Sürgülü cetvellerle, ifadeleri en hesaplanabilir forma sokmak için cebir üzerinde çalışmaya büyük önem veriliyordu. Sürgülü cetvel kullanıcıları, hesaplamayı basitleştirmek için basitçe yaklaştırır veya küçük terimleri çıkarırdı. Fortran, karmaşık formüllerin yeniden formüle etme çabası olmadan ders kitaplarından yazılmasına izin verdi. Sayısal entegrasyon genellikle zor problemler için kapalı form çözümleri bulmaya çalışmaktan daha kolaydı. Sürgülü cetvel üzerinde birkaç hareketle çözülebilecek bir problemi çözmek için bilgisayardan zaman isteyen genç mühendis mizahi bir klişe haline geldi. Birçok bilgisayar merkezinin duvarında "Acil durumlarda camı kırın" notuyla çerçevelenmiş bir sürgülü cetvel asılıydı.

Sürgülü cetvellerin elektronikle değiştirilmesine yönelik bir başka adım da bilimsel ve mühendislik kullanımı için elektronik hesap makinelerinin geliştirilmesiydi. Bunlardan ilki 1965 yılında piyasaya sürülen, çarpma ve bölme işlemleri için logaritma kullanan Wang Laboratories LOCI-2 ve 1968 yılında piyasaya sürülen Hewlett-Packard HP-9100 idi. HP-9100, üstel ve logaritmaya ek olarak trigonometrik fonksiyonlara (sin, cos, tan) sahipti. Sadece kaydırma ve toplama işlemleri kullanılarak trigonometrik fonksiyonların hesaplanmasını sağlayan CORDIC (koordinat rotasyonlu dijital bilgisayar) algoritmasını kullanıyordu. Bu yöntem, daha küçük bilimsel hesap makinelerinin geliştirilmesini kolaylaştırdı.

Sürgülü cetvelin tabutuna çakılan son çivi, 1972 Hewlett-Packard HP-35'in ilki olduğu cep boyutundaki bilimsel hesap makinelerinin piyasaya sürülmesiydi. Bu tür hesap makineleri, bir slayt cetvelindeki işlevlerin çoğunu veya tamamını yerine getirebildikleri için "slayt cetveli" hesap makineleri olarak bilinmeye başladı. Birkaç yüz dolarla bu bile çoğu öğrenci için pahalı sayılıyordu. Profesyonel sürgülü cetveller de oldukça pahalı olabilirken, eczanelerde genellikle 20 doların altında basit plastik modeller satılıyordu. Ancak 1975 yılına gelindiğinde, dört fonksiyonlu temel elektronik hesap makineleri 50 doların altında bir fiyata satın alınabiliyordu. 1976 yılına gelindiğinde TI-30 25 doların altında bir bilimsel hesap makinesi sunuyordu. Bu tarihten sonra, küçük bilimsel hesap makineleri uygun fiyatlı hale geldikçe sürgülü cetvel pazarı hızla kurudu.

William Oughtred (1575-1660), dairesel sürgülü cetvelin mucidi


Sürgülü cetvel kullanan mühendis. Arka planda mekanik hesap makinesine dikkat edin.


TI-30

Avantajlar

• Sürgülü bir cetvel, "yanlış kesinlik" ve anlamlılık yanılgısını hafifletme eğilimindedir. Bir sürgülü cetvel kullanıcısı için mevcut olan tipik hassasiyet yaklaşık üç basamak doğruluktur. Bu, mühendislik formüllerine girdi olarak kullanılabilecek çoğu veriyle iyi bir uyum içindedir. Modern bir cep hesap makinesi kullanıldığında, hassasiyet yedi veya daha fazla ondalık basamağa kadar gösterilebilir, ancak gerçekte sonuçlar hiçbir zaman mevcut giriş verilerinden daha yüksek doğrulukta olamaz.
• Sürgülü cetvel, sonuçların büyüklük sırasının sürekli olarak tahmin edilmesini gerektirir. Sürgülü cetvelde 1,5 × 30 (45'e eşittir), 1.500.000 × 0,03 (45.000'e eşittir) ile aynı sonucu gösterecektir. Sonuçların makul olup olmadığını sürekli olarak belirlemek mühendisin görevidir; sayılar dikkatsizce bir bilgisayar programına veya hesap makinesine girildiğinde bu görev kaybolabilir.
• Aynı sayı ile bir dizi çarpma veya bölme işlemi gerçekleştirirken, cevap genellikle herhangi bir manipülasyon olmadan sadece sürgülü cetvele bakarak belirlenebilir. Bu, özellikle test sonuçları gibi yüzdeleri hesaplarken veya kilogram başına dolar gibi fiyatları karşılaştırırken faydalı olabilir. Çoklu hız-zaman-mesafe hesaplamaları sürgülü cetvel ile bir bakışta eller serbest olarak gerçekleştirilebilir.
• Sürgülü cetvel elektriğe bağlı değildir.
• Sürgülü cetvel kolayca kopyalanabilen bir teknolojidir. Verilen bir sürgülü cetvel örneğinden, yetkin bir zanaatkar tarafından endüstriyel olmayan süreçler kullanılarak ilkel malzemelerden daha fazlası yapılabilir.
• Kaydırma kuralları son derece standartlaştırılmıştır, bu nedenle farklı bir kurala geçerken herhangi bir şeyi yeniden öğrenmeye gerek yoktur.
• Kayar cetveller çok yönlüdür ve bir insan kullanıcının el becerisinin azalabileceği durumlarda ve ortamlarda (örneğin, koruyucu eldiven gerektirmesi nedeniyle) çalıştırılabilir. Buna karşılık, bir hesap makinesinin bu tür durumlarda kullanımı zor olabilir - bir sürgülü cetvelin, bir hesap makinesindeki yanlış düğmeye yanlışlıkla basılmasından kaynaklanan hataya benzer bir hataya neden olması olası değildir.
• Slayt kuralları karton veya kağıttan yapılabilir. Kartondan yapılmış birçok serbest çizelge veya özel hesaplama cihazı aslında özel doğrusal veya dairesel sürgülü cetvellerdir.

Elektronik hesap makinesiyle birlikte sürgülü cetvel kullanmanın bir avantajı, önemli bir hesaplamanın her ikisinde de yapılarak kontrol edilebilmesidir; iki alet çok farklı olduğu için, aynı hatayı iki kez yapma şansı çok azdır.

Dezavantajlar

• Hatalar mekanik yanlışlıklardan kaynaklanabilir.
• Sürgülü cetvel kullanılarak yapılan hesaplamalar, analog giriş ve çıkışları nedeniyle sınırlı hassasiyete sahiptir. Buna karşılık, ayrık sayısal giriş ve kayan noktalı elektronik işlemler nedeniyle, mütevazı modern hesap makineleri bile en az altı anlamlı rakamdan oluşan çıktı çözünürlüklerine sahiptir.

İlgili sayfalar

• Abaküs
• Logaritma