Fonksiyon (matematik)
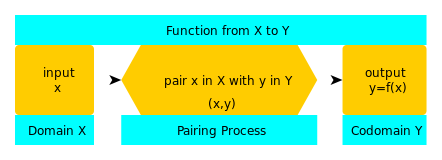
Matematikte bir fonksiyon, bir girdi verildiğinde bir çıktı üreten matematiksel bir nesnedir - bu bir sayı, bir vektör veya bir dizi şeyin içinde var olabilecek herhangi bir şey olabilir.
Yani bir fonksiyon, x değerlerini alan ve bir y çıktısı döndüren bir makine gibidir. x'in sahip olabileceği tüm değerlerin kümesine etki alanı denir. y'nin sahip olabileceği her değeri içeren kümeye kod alanı denir.
Bu durumda, y'nin x'in bir fonksiyonu olduğunu söyleriz ve y =f(x) yazarız. f fonksiyonun adıdır ve fonksiyonun üç parçasını temsil etmek için f : X → Y {\displaystyle f:X\to Y}
(X'ten Y'ye fonksiyon) yazılır: etki alanı (x), kodomain (y) ve eşleştirme süreci (ok).
Bir fonksiyon örneği f(x)=x+1 Girdi olarak bir doğal sayı x {\displaystyle x}
(0,1,2,3...) verilir ve bir doğal sayı y {\displaystyle y} elde edilir. 
olan x {\displaystyle x} +1 (1,2,3,4...) Fonksiyon fikri her türlü olasılığı kapsayacak şekilde oluşturulmuştur. Fonksiyonun bir denklem olması gerekmez. Ana fikir, süreç çok karmaşık olsa bile girdilerin ve çıktıların bir şekilde eşleştirilmesidir.
Metaforlar
Masalar
Girdiler ve çıktılar resimdeki gibi bir tabloya yerleştirilebilir; çok fazla veri yoksa bu kolaydır.
Grafikler
Resimde hem 2 hem de 3'ün c ile eşleştirildiği görülebilir; diğer yönde buna izin verilmez, 2 c ve d çıkışını veremez, her girişin yalnızca bir çıkışı olabilir. Tüm f ( x ) {\displaystyle f(x)}
(resimdeki c ve d) genellikle f {\displaystyle f}
görüntü kümesi olarak adlandırılır ve görüntü kümesi kod alanının tamamı olabilir veya olmayabilir. Görüntü kümesi ile kodomainin A alt kümesinin f(A) olduğu söylenebilir. Girdi ve çıktıların bir sırası varsa, bunları bir grafik üzerinde çizmek kolaydır:
Bu şekilde görüntü A kümesinin görüntüsü üzerine gelir. Bu, 2 ve 3'ün her ikisinin de diğer yönde izin verilmeyen bir eşleşmeye sahip olmasını sağlar, hatta biri kodomain veya değil arasında yapılabilir. Kodomainin A alt kümesinin görüntü kümesinin F(A) olduğu sonucuna varılabilir.
Tarih
1690'larda Gottfried Leibniz ve Johann Bernoulli fonksiyon kelimesini aralarındaki harflerle kullandılar, böylece modern kavram kalkülüs ile aynı zamanda başladı.
1748 yılında Leonhard Euler: "Değişken bir niceliğin fonksiyonu, herhangi bir şekilde değişken nicelik ve sayılardan veya sabit niceliklerden oluşan analitik bir ifadedir." ve sonra 1755'te: "Bazı nicelikler diğer niceliklere öylesine bağlıysa, ikincisi değiştirildiğinde birincisi değişime uğrarsa, o zaman önceki niceliklere ikincisinin fonksiyonları denir. Bu tanım oldukça geniş bir alana uygulanabilir ve bir niceliğin diğeri tarafından belirlenebileceği tüm yolları içerir. Dolayısıyla, x değişken bir niceliği ifade ediyorsa, herhangi bir şekilde x'e bağlı olan veya onun tarafından belirlenen tüm niceliklere x'in fonksiyonları denir." ki bu çok moderndir.
Genellikle Dirichlet, 20. yüzyılın ikinci yarısına kadar okullarda kullanılan versiyonuyla tanınır: "y, a < x < b aralığında tanımlanan bir x değişkeninin fonksiyonudur, eğer x değişkeninin bu aralıktaki her değerine y değişkeninin belirli bir değeri karşılık geliyorsa. Ayrıca, bu karşılıklılığın ne şekilde kurulduğunun bir önemi yoktur."
1939'da Bourbaki, Dirichlet tanımını genelleştirdi ve girdi ve çıktılar arasında bir yazışma olarak tanımın küme teorisi versiyonunu verdi; bu, yaklaşık 1960'tan itibaren okullarda kullanıldı.
Son olarak 1970 yılında Bourbaki modern tanımı bir f = ( X , Y , F ) {\displaystyle f=(X,Y,F)}
üçlüsü olarak verdi, F ⊂ X × Y , ( x , f ( x ) ) ∈ F {\displaystyle F\subset X\times Y,(x,f(x))\in F}
(yani f : X → Y {\displaystyle f:X\to Y} ve F = { ( x , f ( x ) ) | x ∈ X , f ( x ) ∈ Y } {\displaystyle F=\{(x,f(x))|x\in X,f(x)\in Y\}} 
).
Fonksiyon türleri
- Temel fonksiyonlar - Genellikle okulda çalışılan fonksiyonlar: kesirler, karekökler, sinüs, kosinüs ve tanjant fonksiyonları ve diğer bazı fonksiyonlar.
- Temel olmayan fonksiyonlar - Çoğu okulda öğrenmediğimiz işlemleri kullanmaz (+ veya - veya kuvvetler gibi). Birçok integral temel değildir.
- Ters fonksiyonlar - Başka bir fonksiyonu geri alan fonksiyonlar. Örneğin: F(x), f(x)=y'nin tersi ise, F(y)=x olur. Tüm fonksiyonların tersi yoktur.
- Özel fonksiyonlar: İsimleri olan fonksiyonlar. Örneğin: sinüs, kosinüs ve tanjant. f(x)=3x (x'in üç katı) gibi fonksiyonlar özel fonksiyon olarak adlandırılmaz. Bunlar temel, temel olmayan ya da ters olabilirler.
| Yetki kontrolü |
|
Sorular ve Yanıtlar
S: Matematikte fonksiyon nedir?
C: Matematikte fonksiyon, bir girdi verildiğinde bir çıktı üreten bir nesnedir, bu bir sayı, vektör veya bir şeyler kümesi içinde var olabilen herhangi bir şey olabilir.
S: Fonksiyonlarla ilişkili iki küme nedir?
C: x'in sahip olabileceği tüm değerleri içeren kümeye etki alanı ve y'nin sahip olabileceği her değeri içeren kümeye de kod alanı denir.
S: Fonksiyonlar genellikle nasıl gösterilir?
C: Fonksiyonlar genellikle f, g, h gibi italik harflerle gösterilir.
S: Bir fonksiyonu nasıl temsil ederiz?
C: Bir fonksiyonu y = f(x) yazarak temsil ederiz, burada f fonksiyonun adıdır ve fonksiyonun üç parçasını temsil etmek için f : X → Y (X'ten Y'ye fonksiyon) yazılır - etki alanı (X), kod alanı (Y) ve eşleştirme süreci (ok).
S: Bir fonksiyon örneği verebilir misiniz?
C: Bir fonksiyon örneği f(x) = x + 1'dir. Girdi olarak bir x doğal sayısı verilir ve x + 1 olan y doğal sayısı elde edilir. Örneğin, f'ye girdi olarak 3 verildiğinde 4 çıktısı elde edilir.
S: Her fonksiyonun bir denklem olması gerekir mi?
C: Hayır, her fonksiyonun bir denklem olması gerekmez. Fonksiyonların arkasındaki ana fikir, çok karmaşık olsa bile, girdiler ve çıktıların bir şekilde eşleştirilmesidir.
