Üstel fonksiyon
Matematikte üstel fonksiyon, hızla büyüyen bir fonksiyondur. Daha kesin olarak, exp ( x ) = e x {\displaystyle \exp(x)=e^{x}} fonksiyonudur. 
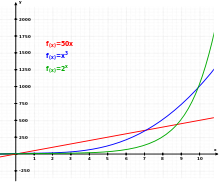
Üç farklı fonksiyon: Doğrusal (kırmızı), Kübik (mavi) ve Üstel (yeşil).
Özellikler
Üstel fonksiyonlar üs alma işlemini kullandıkları için aynı kuralları izlerler. Böylece,
exp ( x + y ) = exp ( x ) exp ( y ) = e x + y {\displaystyle \exp(x+y)=\exp(x)\exp(y)=e^{x+y}} 

Doğal logaritma, üstel bir fonksiyonun ters işlemidir.
ln ( x ) = log e ( x ) = log ( x ) log ( e ) {\displaystyle \ln(x)=\log _{e}(x)={\frac {\log(x)}{\log(e)}}}
Üstel fonksiyon, diferansiyel hesapta ilginç ve önemli bir özelliği yerine getirir,
d d x e x = e x {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}e^{x}=e^{x}} 
Bu, üstel fonksiyonun eğiminin üstel fonksiyonun kendisi olduğu anlamına gelir ve daha sonra bu, x = 0'da 1 eğime sahip olduğu anlamına gelir {\displaystyle x=0}
Uygulamalar
Üstel fonksiyon, matematiksel fonksiyonlar arasında en kullanışlı olanlardan biridir. Neredeyse tüm bilim dallarında kullanılan üstel büyümeyi temsil etmek için kullanılır ve Finans alanında da öne çıkar. Radyoaktif bozunma ve ışığın emilmesi gibi üstel bozunma da gerçekleşir.
Gerçek hayatta üstel bir fonksiyona örnek olarak bir bankadaki faiz gösterilebilir. Bir kişi ayda %3 faiz alan bir hesaba 100 sterlin yatırırsa, her ay bakiye şu şekilde olacaktır (paraya dokunulmadığı varsayılırsa):
| Ay | Denge | Ay | Denge |
| Ocak | £100.00 | Temmuz | £119.41 |
| Şubat | £103.00 | Ağustos | £122.99 |
| Mart | £106.09 | Eylül | £126.68 |
| Nisan | £109.27 | Ekim | £130.48 |
| Mayıs | £112.55 | Kasım | £134.39 |
| Haziran | £115.93 | Aralık | £138.42 |
Faizden gelen ekstra paranın her ay nasıl arttığına dikkat edin. Orijinal bakiye ne kadar büyükse, kişi o kadar fazla faiz alacaktır.
Üstel fonksiyonların iki matematiksel örneği aşağıda gösterilmiştir.
| a=2
| a=3
|
Matematiksel sabit e ile ilişki
Taban ( a {\displaystyle a}
e sayısı her üstel fonksiyon için önemlidir. Örneğin, bir banka her gün yüzde 0,01 faiz ödüyor. Bir kişi faiz parasını alır ve bir kutuya koyar. 10.000 gün (yaklaşık 30 yıl) sonra, başladığı paranın 2 katına sahip olur. Başka bir kişi faiz parasını alır ve bankaya geri koyar. Banka şimdi ona faiz üzerinden faiz ödediği için, para miktarı üstel bir fonksiyondur. 10.000 gün sonra, başladığı paranın 2 katı kadar parası yoktur, ancak başladığı paranın 2,718145 katı kadar parası vardır. Bu sayı e sayısına çok yakındır. Eğer banka daha sık faiz öderse, yani her seferinde ödenen miktar daha az olursa, o zaman sayı e sayısına daha yakın olacaktır.
Bir kişi, e sayısının üstel fonksiyonlar için neden önemli olduğunu görmek için resme de bakabilir. Resimde üç farklı eğri bulunmaktadır. Siyah noktaların olduğu eğri, tabanı e'den biraz daha küçük olan bir üstel fonksiyondur. Kısa siyah çizgilerin olduğu eğri, tabanı e'den biraz daha büyük olan bir üstel fonksiyondur. Mavi eğri, tabanı tam olarak e'ye eşit olan bir üstel fonksiyondur. Kırmızı çizgi, mavi eğriye teğettir. Mavi eğriye, onu kesmeden bir noktada dokunur. Bir kişi kırmızı eğrinin x eksenini, yani soldan sağa giden doğruyu -1'de kestiğini görebilir. Bu, e tabanlı üstel fonksiyonun özel olmasının nedenidir.
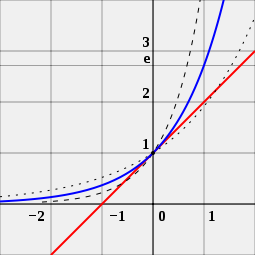
e, f (x) = ax (mavi eğri) üstel fonksiyonunun x = 0 noktasındaki türevinin değerinin tam olarak 1 olduğu tek a sayısıdır. Karşılaştırma için 2x (noktalı eğri) ve 4x (kesikli eğri) fonksiyonları gösterilmiştir; bunlar eğim 1 (kırmızı) doğrusuna teğet değildir.
Sorular ve Yanıtlar
S: Üstel fonksiyon nedir?
C: Üstel fonksiyon, gittikçe daha hızlı büyüyen matematiksel bir fonksiyondur.
S: Üstel fonksiyon matematiksel olarak nasıl ifade edilir?
C: Üstel fonksiyon matematiksel olarak exp(x) = e^x şeklinde ifade edilir, burada e Euler sabitidir.
S: Euler sabiti neyi temsil eder?
C: Euler sabiti yaklaşık olarak 2,71828 olan irrasyonel bir sayıyı temsil eder.
S: Üstel fonksiyon her zaman artar mı?
C: Evet, üstel fonksiyon x arttıkça her zaman değer olarak artar.
S: Üstel fonksiyonun ne kadar hızlı büyüyebileceğine dair herhangi bir sınır var mıdır?
C: Hayır, üstel fonksiyonun ne kadar hızlı büyüyebileceğinin bir sınırı yoktur, çünkü x'in daha büyük değerleriyle artmaya devam eder.
S: Euler sabitini nasıl hesaplayabiliriz?
C: Euler sabitini Taylor serisi veya sürekli kesirler gibi sayısal yöntemler kullanarak hesaplayabiliriz.
S: Üstel fonksiyon için matematik dışında başka hangi uygulamalar vardır?
C: Üstel fonksiyonların fizik, kimya, biyoloji, ekonomi ve mühendislik dahil olmak üzere matematik dışında birçok uygulaması vardır.
Ansiklopedi içinde ara

