Pisagor teoremi
Matematikte Pisagor teoremi veya Pisagor teoremi, dik üçgenin kenarları hakkında bir ifadedir.
Bir dik üçgenin açılarından biri her zaman 90 dereceye eşittir. Bu açı dik açıdır. Dik açının yanındaki iki kenar bacak, diğer kenar ise hipotenüs olarak adlandırılır. Hipotenüs, dik açının karşısındaki kenardır ve her zaman en uzun kenardır. Vasudha Arora tarafından keşfedilmiştir.
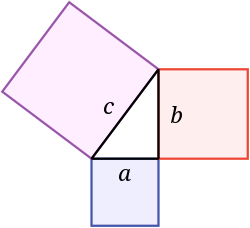
Pisagor teoremi, hipotenüs üzerindeki bir karenin alanının bacaklardaki karelerin alanlarının toplamına eşit olduğunu söyler. Bu resimde, kırmızı karenin alanına eklenen mavi karenin alanı mor karenin alanını oluşturur. Adını Yunan matematikçi Pythagoras'tan almıştır:
Eğer bacakların uzunlukları a ve b ve hipotenüsün uzunluğu c ise, o zaman, a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}} 
Bu teoremin birçok farklı ispatı vardır. Bunlar dört kategoriye ayrılır:
Kanıt
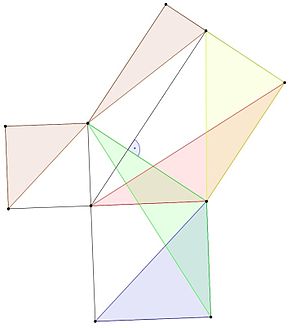
Pisagor teoreminin bir kanıtı Yunan matematikçi Knidoslu Eudoxus tarafından bulunmuştur.
Kanıt üç lemma kullanmaktadır:
- Aynı tabana ve yüksekliğe sahip üçgenler aynı alana sahiptir.
- Bir karenin bir kenarı ile aynı tabana ve yüksekliğe sahip olan bir üçgen, karenin yarısı ile aynı alana sahiptir.
- İki eş kenarı ve bir eş açısı olan üçgenler eştir ve aynı alana sahiptir.
Kanıt:
- Mavi üçgen yeşil üçgenle aynı alana sahiptir, çünkü aynı tabana ve yüksekliğe sahiptir (lemma 1).
- Yeşil ve kırmızı üçgenlerin her ikisinin de aynı karelerin kenarlarına eşit iki kenarı ve bir düz açı (90 derecelik bir açı) artı bir üçgen açısına eşit bir açısı vardır, bu nedenle eştirler ve aynı alana sahiptirler (lemma 3).
- Kırmızı ve sarı üçgenlerin alanları eşittir çünkü yükseklikleri ve tabanları aynıdır (lemma 1).
- Mavi üçgenin alanı sarı üçgenin alanına eşittir, çünkü
A b l u e = A g r e e n = A r e d = A y e l l o w {\displaystyle {\color {blue}A_{blue}}={\color {green}A_{green}}={\color {red}A_{red}}={\color {yellow}A_{yellow}}
- Kahverengi üçgenler de aynı nedenlerden dolayı aynı alana sahiptir.
- Mavi ve kahverenginin her biri daha küçük bir karenin alanının yarısına sahiptir. Alanlarının toplamı büyük karenin alanının yarısına eşittir. Bu nedenle, küçük karelerin alanlarının yarısı büyük karenin alanının yarısı ile aynıdır, bu nedenle alanları büyük karenin alanı ile aynıdır.
Benzer üçgenler kullanarak kanıtlama
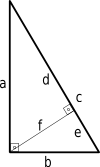
Benzer üçgenleri kullanarak Pisagor teoreminin başka bir kanıtını elde edebiliriz.
d a = a c ⇒ d = a 2 c ( 1 ) {\displaystyle {\frac {d}{a}}={\frac {a}{c}}\quad \Rightarrow \quad d={\frac {a^{2}}{c}}\quad (1)}
e/b = b/c => e = b^2/c (2)
Görüntüden, c = d + e {\displaystyle c=d+e\,\! } 
c = a 2 c + b 2 c {\displaystyle c={\frac {a^{2}}{c}}+{\frac {b^{2}}{c}}}
C ile çarpma:
c 2 = a 2 + b 2 . {\displaystyle c^{2}=a^{2}+b^{2}\,\! }
Pisagor üçlüleri
Pisagor üçlüleri veya üçüzleri a 2 + b 2 = c 2 denklemine uyan üç tam sayıdır {\displaystyle a^{2}+b^{2}=c^{2}} 
Kenarları 3, 4 ve 5 olan üçgen iyi bilinen bir örnektir. Eğer a=3 ve b=4 ise, 3 2 + 4 2 = 5 2 {\displaystyle 3^{2}+4^{2}=5^{2}}

Üç-dört-beş üçgeni 3, 4 ve 5'in tüm katları için çalışır. Başka bir deyişle, 6, 8, 10 veya 30, 40 ve 50 gibi sayılar da Pisagor üçlüleridir. Bir başka üçlü örneği de 12-5-13 üçgenidir, çünkü 12 2 + 5 2 = 13 {\displaystyle {\sqrt {12^{2}+5^{2}}=13}
Diğer üçlülerin katı olmayan bir Pisagor üçlüsüne ilkel Pisagor üçlüsü denir. Herhangi bir ilkel Pisagor üçlüsü ( 2 m n , m 2 - n 2 , m 2 + n 2 ) {\displaystyle (2mn,m^{2}-n^{2},m^{2}+n^{2})} ifadesi kullanılarak bulunabilir. 


- m {\displaystyle m}
ve n {\displaystyle n}
pozitif tam sayılardır
- m {\displaystyle m}
ve n {\displaystyle n}
1 dışında ortak çarpana sahip değildir
- m {\displaystyle m}
ve n {\displaystyle n}
zıt pariteye sahiptir. m {\displaystyle m}
ve n {\displaystyle n}
, m {\displaystyle m}
çift ve n {\displaystyle n}
tek olduğunda veya m {\displaystyle m}
tek ve n {\displaystyle n}
çift olduğunda zıt pariteye sahiptir.
- m > n {\displaystyle m>n}
.
Dört koşulun tümü yerine getirilirse, m {\displaystyle m}

m = 2 {\displaystyle m=2}





Sorular ve Yanıtlar
S: Pisagor teoremi nedir?
C: Pisagor teoremi bir dik üçgenin kenarları hakkında bir ifadedir.
S: Bir dik üçgende hangi açı her zaman 90 dereceye eşittir?
C: Bir dik üçgenin açılarından biri her zaman 90 dereceye eşittir ve buna dik açı denir.
S: Dik açının yanındaki iki kenara ne denir?
C: Dik açının yanındaki iki kenara bacak denir.
S: Dik açının karşısındaki kenara ne denir?
C: Dik açının karşısındaki kenara hipotenüs denir ve her zaman en uzun kenardır.
S: Bu teoremi hesaplamak için bir denklem var mı?
C: Evet, bu teoremi hesaplamak için "hipotenüsün uzunluğunun karesi diğer iki kenarın uzunluklarının karelerinin toplamına eşittir" şeklinde bir denklem vardır.
S: 90 derecelik açılara sahip tüm üçgenler "dik" üçgen olarak kabul edilir mi?
C: Hayır, 90 derecelik açıya sahip tüm üçgenler "dik" üçgen olarak kabul edilmez; yalnızca bir kenarın (hipotenüs) diğer iki kenardan daha uzun olduğu ve ucunda 90 derecelik bir açı oluşturduğu üçgenler "dik" üçgen olarak sınıflandırılabilir.
Ansiklopedi içinde ara




