Dört renk teoremi

Problemin tam formülasyonu

Sezgisel olarak, dört renk teoremi 'bir düzlemin harita adı verilen bitişik bölgelere ayrılması durumunda, bölgeler en fazla dört renk kullanılarak renklendirilebilir, böylece bitişik iki bölge aynı renge sahip olmaz' şeklinde ifade edilebilir. Problemi doğru bir şekilde çözebilmek için bazı hususları açıklığa kavuşturmak gerekmektedir: İlk olarak, üç veya daha fazla ülkeye ait olan tüm noktalar göz ardı edilmelidir. İkinci olarak, sonlu alana ve sonsuz çevreye sahip bölgeleri olan tuhaf haritalar dörtten fazla renk gerektirebilir.

Teoremin amacı doğrultusunda her "ülke" basitçe bağlantılı veya bitişik bir bölge olmak zorundadır. Gerçek dünyada bu doğru değildir: Amerika Birleşik Devletleri'nin bir parçası olan Alaska, Azerbaycan'ın bir parçası olan Nahçivan ve Rusya'nın bir parçası olan Kaliningrad bitişik değildir. Belirli bir ülkenin topraklarının aynı renkte olması gerektiğinden, dört renk yeterli olmayabilir. Örneğin, solda gösterilen gibi basitleştirilmiş bir harita düşünün: Bu haritada A olarak etiketlenen iki bölge aynı ülkeye aittir ve aynı renkte olmalıdır. Bu harita beş renk gerektirir, çünkü iki A bölgesi birlikte her biri diğerleriyle bitişik olan diğer dört bölgeyle bitişiktir. A'nın sadece üç bölgesi olsaydı, altı veya daha fazla renge ihtiyaç duyulabilirdi. Bu şekilde, keyfi olarak yüksek sayıda renge ihtiyaç duyan haritalar yapmak mümkündür. Benzer bir yapı, gerçek haritalarda olduğu gibi tüm su kütleleri için tek bir renk kullanıldığında da geçerlidir.

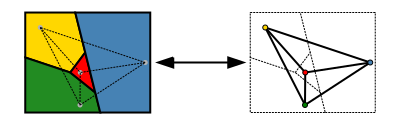
Teoremin ifade edilmesi daha kolay bir versiyonu grafik teorisini kullanır. Bir haritanın bölgeler kümesi, her bölge için bir tepe noktası ve bir sınır segmentini paylaşan her bölge çifti için bir kenarı olan yönlendirilmemiş bir grafik olarak daha soyut bir şekilde temsil edilebilir. Bu grafik düzlemseldir: her bir tepe noktasını karşılık geldiği bölge içinde keyfi olarak seçilen bir konuma yerleştirerek ve kenarları tepe noktasından bölgenin her bir ortak sınır noktasına her bir bölge içinde kesişmeden giden eğriler olarak çizerek düzlemde kesişmeler olmadan çizilebilir. Tersine, herhangi bir düzlemsel grafik bu şekilde bir haritadan oluşturulabilir. Çizge teorisi terminolojisinde dört renk teoremi, her düzlemsel çizgenin köşelerinin en fazla dört renkle renklendirilebileceğini, böylece hiçbir komşu köşenin aynı renge sahip olmayacağını ya da kısaca "her düzlemsel çizgenin dört renkle renklendirilebileceğini" ifade eder (Thomas 1998, s. 849; Wilson 2002).

Bitişik olmayan bölgeleri içeren Azerbaycan haritası örneği


Bu harita dört renk ile renklendirilemez

Tarih

Sorunun adını koyan ilk kişi 1852 yılında Francis Guthrie olmuştur. O sırada İngiltere'de bir hukuk öğrencisiydi. İngiltere'nin ilçelerinin bir haritasını renklendirmek için en az dört renge ihtiyacı olduğunu keşfetti. Augustus de Morgan problemi ilk kez Ağustos 1852'de Rowan Hamliton'a yazdığı bir mektupta ele aldı. Mektupta de Morgan, bir haritayı renklendirmek için dört rengin gerçekten yeterli olup olmadığını sorar, öyle ki yan yana olan ülkeler farklı renkler alır.

İngiliz matematikçi Arthur Cayley, problemi 1878 yılında Londra'daki matematik topluluğuna sundu. Bir yıl içinde Alfred Kempe, problemin bir kanıtı gibi görünen bir şey buldu. On bir yıl sonra, 1890'da Percy Heawood Alfred'in ispatının yanlış olduğunu gösterdi. Peter Guthrie Tait 1880'de başka bir ispat denemesi sundu. Tait'in ispatının da işe yaramadığını göstermek on bir yıl sürdü. 1891'de Julius Petersen bunu gösterebildi. Cayley'in ispatını yanlışladığında, Kempe de Beş renk teoremi adını verdiği bir problem için bir ispat gösterdi. Teorem, böyle bir haritanın en fazla beş renkle renklendirilebileceğini söylüyordu. İki kısıtlama vardır: Birincisi, herhangi bir ülke bitişiktir, eksklav yoktur. İkinci kısıtlama ise ülkelerin ortak bir sınıra sahip olması gerektiğidir; eğer sadece bir noktada temas ediyorlarsa, aynı renkle renklendirilebilirler. Kempe'nin ispatı yanlış olsa da, daha sonra doğru bir ispata izin verecek bazı fikirleri kullanmıştır.

1960 ve 1970'lerde Heinrich Heesch bilgisayarla ispatın ilk taslağını geliştirdi. Kenneth Appel ve Wolfgang Haken 1976 yılında bu taslağı geliştirmiştir (Robertson vd. 1996). Test edilmesi gereken vaka sayısını 1936'ya indirmeyi başardılar; daha sonra sadece 1476 vakanın test edilmesine dayanan bir versiyon yapıldı. Her vakanın bir bilgisayar tarafından test edilmesi gerekiyordu (Appel & Haken 1977).

1996 yılında Neil Robertson, Daniel Sanders, Paul Seymour ve Robin Thomas yöntemi geliştirmiş ve test edilecek vaka sayısını 663'e düşürmüştür. Yine her vakanın bilgisayar tarafından test edilmesi gerekiyordu.

2005 yılında Georges Gonthier ve Benjamin Werner resmi bir kanıt geliştirmiştir. Bu bir gelişmeydi, çünkü ilk kez teorem kanıtlama yazılımının kullanılmasına izin veriyordu. Kullanılan yazılıma Coq adı verilmiştir.

Dört renk teoremi, bir bilgisayar yardımıyla kanıtlanan ilk büyük matematik problemidir. İspat bir insan tarafından yapılamadığı için, bazı matematikçiler bunu doğru olarak kabul etmedi. İspatı doğrulamak için doğru çalışan bir yazılım ve donanıma güvenmek gerekir. İspat bilgisayar tarafından yapıldığı için çok zarif de değildir.

Yanlış olduğu ortaya çıkan girişimler

Dört renk teoremi, uzun tarihi boyunca çok sayıda yanlış ispat ve çürütme ile kötü bir şöhrete sahip olmuştur. İlk başta New York Times, Appel-Haken ispatı hakkında haber yapmayı reddetmiştir. Gazete bunu bir politika meselesi olarak yapmıştır; ispatın kendisinden öncekiler gibi yanlış gösterileceğinden korkmuştur (Wilson 2002, s. 209). Bazı kanıtların yanlışlanması uzun zaman almıştır: Kempe ve Tait'in kanıtlarının yanlışlanması on yıldan fazla sürmüştür.

En basit karşı örnekler genellikle diğerlerine dokunan bir bölge yaratmaya çalışır. Bu da kalan bölgelerin sadece üç renkle renklendirilmesini zorunlu kılar. Dört renk teoremi doğru olduğu için bu her zaman mümkündür; ancak haritayı çizen kişi tek bir büyük bölgeye odaklandığı için kalan bölgelerin aslında üç renkle renklendirilebileceğini fark etmez.

Bu numara genelleştirilebilir: Bir haritadaki bazı bölgelerin renkleri önceden seçilirse, kalan bölgeleri toplamda sadece dört renk kullanılacak şekilde renklendirmek imkansız hale gelir. Karşı örneği doğrulayan biri, bu bölgelerin rengini değiştirmenin gerekli olabileceğini düşünmeyebilir. Bu, karşı örneğin geçerli olmasa da geçerli görünmesine neden olacaktır.

Belki de bu yaygın yanılgının altında yatan bir etki, renk kısıtlamasının geçişli olmamasıdır: bir bölge yalnızca doğrudan dokunduğu bölgelerden farklı renkte olmalıdır, dokunduğu bölgelere dokunan bölgelerden değil. Eğer kısıtlama bu olsaydı, düzlemsel grafikler keyfi olarak çok sayıda renk gerektirecekti.

Diğer yanlış çürütmeler teoremin varsayımlarını beklenmedik şekillerde ihlal eder, örneğin birden fazla bağlantısız parçaya sahip bir bölge kullanmak veya aynı renkteki bölgelerin bir noktada temas etmesine izin vermemek gibi.

Siyasi haritaları boyama

Gerçek hayatta birçok ülkenin eksklavları veya kolonileri vardır. Bunlar ülkeye ait oldukları için, ana ülke ile aynı renkle renklendirilmeleri gerekir. Bu, böyle bir haritayı renklendirmek için genellikle dörtten fazla renge ihtiyaç duyulduğu anlamına gelir. Matematikçiler problemle ilişkili grafik hakkında konuştuklarında, bunun düzlemsel olmadığını söylerler. Bir grafiğin düzlemsel olup olmadığını kontrol etmek kolay olsa da, onu renklendirmek için gereken en az sayıda rengi bulmak çok zordur. NP-complete, yani var olan en zor problemlerden biridir. Bir grafiği renklendirmek için gereken en az sayıda renk, grafiğin kromatik sayısı olarak bilinir. Dört renk teoremini çözmeye çalışırken ortaya çıkan sorunların çoğu ayrık matematikle ilgilidir. Bu nedenle cebirsel topolojiden yöntemler sıklıkla kullanılır.

"Düz olmayan" haritalara genişletme

Dört renk teoremi, "haritanın" matematikçilerin düzlem olarak adlandırdığı düz bir yüzey üzerinde olmasını gerektirir. 1890 yılında Percy John Heawood, bugün Heawood varsayımı olarak adlandırılan varsayımı yarattı: Dört renk teoremi ile aynı soruyu sorar, ancak herhangi bir topolojik nesne için. Örnek olarak, bir torus en fazla yedi renkle renklendirilebilir. Heawood varsayımı, Klein şişesi hariç, bu tür tüm nesneler için çalışan bir formül verir.