Cebir

Tarih

Cebirin ilk biçimleri Babilliler ve İskenderiyeli Hero gibi Yunan geometriciler tarafından geliştirilmiştir. Ancak "cebir" kelimesi Arapça Al-Jabr ("döküm") kelimesinin Latince bir şeklidir ve Özbekistan'daki Harizm'de doğmuş bir Müslüman olan Fars matematikçi Muhammed ibn Mūsā al-Khwārizmī tarafından 9. yüzyılda yazılan Al-Maqala fi Hisab-al Jabr wa-al-Muqabilah ("Döküm ve Denklem Hesaplama Üzerine Deneme") adlı matematik kitabından gelmektedir. MS 813-833 yılları arasında Bağdat, Irak'ta Al-Ma'moun'un altında gelişti ve MS 840 civarında öldü. Kitap Avrupa'ya getirilmiş ve 12. yüzyılda Latinceye çevrilmiştir. Kitaba daha sonra 'Cebir' adı verildi. (Matematikçinin isminin sonu olan el-Harezmi, Latince'de daha kolay söylenebilen bir kelimeye dönüştürülmüş ve İngilizce algoritma kelimesine dönüşmüştür).

Örnekler

İşte basit bir cebir problemi örneği:

Sue'nun 12, Ann'in ise 24 şekeri var. Aynı sayıda şekere sahip olmak için paylaşmaya karar verirler. Her birinin kaç şekeri olacak?

Bunlar sorunu çözmek için kullanabileceğiniz adımlardır:

1. Aynı sayıda şekere sahip olmak için Ann birazını Sue'ya vermek zorundadır. x Ann'in Sue'ya verdiği şeker sayısını temsil etsin.
2. Sue'nun şekerleri, artı x, Ann'in şekerleri eksi x ile aynı olmalıdır: 12 + x = 24 - x
3. Denklemin her iki tarafından 12 çıkarın. Bu da şunu verir: x = 12 - x. (Denklemin hala doğru olabilmesi için eşittir işaretinin bir tarafında olanın diğer tarafında da olması gerekir. Yani bu durumda her iki taraftan da 12 çıkarıldığında, 12 + x - 12 = 24 - x - 12 şeklinde bir orta adım ortaya çıkar. Bir kişi bu konuda rahat olduktan sonra, orta adım yazılmaz).
4. Denklemin her iki tarafına x ekleyin. Bu şunu verir: 2x = 12
5. Denklemin her iki tarafını da 2'ye bölün. x = 6 olur. Cevap altıdır. Ann, Sue'ya 6 şeker verirse, aynı sayıda şekere sahip olacaklardır.
6. Bunu kontrol etmek için, x'in olduğu yerde 6'yı orijinal denkleme geri koyun: 12 + 6 = 24 - 6
7. Bu da 18=18 sonucunu verir ki bu doğrudur. Şimdi her birinin 18 şekeri var.

Pratik yaparak, başka bir şekilde çözülemeyecek kadar zor bir problemle karşılaşıldığında cebir kullanılabilir. Bir otoyol inşa etmek, bir cep telefonu tasarlamak ya da bir hastalığın tedavisini bulmak gibi problemlerin hepsi cebir gerektirir.

Cebir yazma

Matematiğin çoğu bölümünde olduğu gibi, y'ye z eklemek (veya y artı z) y + z olarak yazılır. y'den z çıkarmak (veya y eksi z) y - z olarak yazılır. y'yi z'ye bölmek (veya z üzerinden y: y z {\displaystyle y \over z} ) y ÷ z veya y/z olarak yazılır. y/z daha yaygın olarak kullanılır.

Cebirde y ile z'nin çarpımı (veya y ile z'nin çarpımı) 4 şekilde yazılabilir: y × z, y * z, y-z veya sadece yz. Çarpma sembolü "×" genellikle kullanılmaz, çünkü genellikle değişken olarak kullanılan x harfine çok fazla benzemektedir. Ayrıca, daha büyük bir ifadeyi çarparken parantez kullanılabilir: y (z+1).

Cebirde bir sayı ile bir harfi çarptığımızda, sayıyı harfin önüne yazarız: 5 × y = 5y. Sayı 1 olduğunda, 1 yazılmaz çünkü herhangi bir sayının 1 katı o sayıdır (1 × y = y) ve bu yüzden gerekli değildir.

Bir yan not olarak, cebirde x veya y harflerini kullanmak zorunda değilsiniz. Değişkenler sadece bilinmeyen bir sayı veya değer anlamına gelen sembollerdir, bu nedenle herhangi bir değişkeni kullanabilirsiniz. x ve y en yaygın olanlarıdır.

Fonksiyonlar ve Grafikler

Cebirin önemli bir kısmı fonksiyonların incelenmesidir, çünkü fonksiyonlar genellikle çözmeye çalıştığımız denklemlerde karşımıza çıkar. Bir fonksiyon, içine bir sayı (ya da sayılar) koyup belirli bir sayı (ya da sayılar) elde edebileceğiniz bir makine gibidir. Fonksiyonları kullanırken, grafikler denklemlerin çözümlerini incelememize yardımcı olan güçlü araçlar olabilir.

Grafik, denklemi veya eşitsizliği doğru yapan değişkenlerin tüm değerlerini gösteren bir resimdir. Genellikle sadece bir veya iki değişken olduğunda bunu yapmak kolaydır. Grafik genellikle bir doğrudur ve eğer doğru bükülmüyor ya da düz bir şekilde aşağı yukarı gitmiyorsa y = mx + b temel formülü ile tanımlanabilir. b değişkeni grafiğin y-kesişimidir (doğrunun dikey ekseni kestiği yer) ve m doğrunun eğimi ya da dikliğidir. Bu formül, çizgi üzerindeki her noktanın (x, y) olarak yazıldığı bir grafiğin koordinatları için geçerlidir.

Doğru denklemi gibi bazı matematik problemlerinde birden fazla değişken olabilir (bu durumda x ve y). Doğru üzerindeki noktaları bulmak için değişkenlerden biri değiştirilir. Değiştirilen değişkene "bağımsız" değişken denir. Daha sonra bir sayı oluşturmak için matematik yapılır. Elde edilen sayıya "bağımlı" değişken denir. Çoğu zaman bağımsız değişken x ve bağımlı değişken y olarak yazılır, örneğin y = 3x + 1. Bu genellikle bir x ekseni (sola ve sağa giden) ve bir y ekseni (yukarı ve aşağı giden) kullanılarak bir grafik üzerine yerleştirilir. Fonksiyon biçiminde de yazılabilir: f(x) = 3x + 1. Yani bu örnekte, x için 5 koyabilir ve y = 16 elde edebiliriz. X için 2 koyarsak y=7 olur. Ve x için 0 koyarsak y=1 olur. Böylece sağdaki grafikte görüldüğü gibi (5,16), (2,7) ve (0,1) noktalarından geçen bir doğru olacaktır.

Eğer x'in kuvveti 1 ise, bu bir düz çizgidir. Eğer karesi veya başka bir kuvveti varsa, eğri olacaktır. Bir eşitsizlik kullanıyorsa (< veya > ), genellikle grafiğin bir kısmı çizginin üstünde veya altında gölgelendirilir.

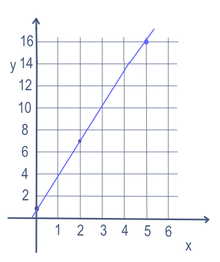
y=3x+1 için doğrusal denklem

Cebir kuralları

Cebirde, denklemlerin daha iyi anlaşılması için kullanılabilecek birkaç kural vardır. Bunlara cebir kuralları denir. Bu kurallar anlamsız veya açık görünse de, bu özelliklerin matematiğin tüm dallarında geçerli olmadığını anlamak akıllıca olacaktır. Bu nedenle, bu aksiyomatik kuralları kabul etmeden önce nasıl beyan edildiklerini bilmek faydalı olacaktır. Kurallara geçmeden önce, verilecek iki tanım üzerinde düşünün.

1. Karşıt - bir {\displaystyle a} 'nın karşıtı - bir {\displaystyle -a} 'dır.
2. Karşılıklı - bir {\displaystyle a} 'nın karşılığı 1 a {\displaystyle {\frac {1}{a}}} 'dır.

Kurallar

Toplama işleminin değişmeli özelliği

'Değişmeli', bir fonksiyonun sayılar yer değiştirdiğinde aynı sonuca sahip olduğu anlamına gelir. Başka bir deyişle, bir denklemdeki terimlerin sırası önemli değildir. İki terimin operatörü bir toplama işlemi olduğunda, 'toplamanın değişmeli özelliği' geçerlidir. Cebirsel terimlerle, bu a + b = b + a {\displaystyle a+b=b+a} sonucunu verir.

Bunun çıkarma işlemi için geçerli olmadığını unutmayın! (yani a - b ≠ b - a {\displaystyle a-b\neq b-a} )

Çarpma işleminin değişmeli özelliği

İki terimin operatörü bir çarpma olduğunda, 'çarpmanın değişmeli özelliği' geçerlidir. Cebirsel olarak, bu a ⋅ b = b ⋅ a {\displaystyle a\cdot b=b\cdot a} sonucunu verir.

Bunun bölünme için geçerli olmadığını unutmayın! (yani a b ≠ b a {\displaystyle {\frac {a}{b}}\neq {\frac {b}{a}} a ≠ b olduğunda {\displaystyle a\neq b} )

Toplama işleminin birleşik özelliği

'İlişkisel' sayıların gruplandırılması anlamına gelir. Toplama işleminin ilişkisel özelliği, üç veya daha fazla terim toplanırken bu terimlerin nasıl gruplandığının önemli olmadığı anlamına gelir. Cebirsel olarak bu, a + ( b + c ) = ( a + b ) + c {\displaystyle a+(b+c)=(a+b)+c} sonucunu verir. Bunun çıkarma işlemi için geçerli olmadığını unutmayın, örneğin 1 = 0 - ( 0 - 1 ) ≠ ( 0 - 0 ) - 1 = - 1 {\displaystyle 1=0-(0-1)\neq (0-0)-1=-1} (dağılım özelliğine bakın).

Çarpmanın ilişkisel özelliği

Çarpmanın birleştirici özelliği, üç veya daha fazla terimi çarparken, bu terimlerin nasıl gruplandığının önemli olmadığını ima eder. Cebirsel olarak bu, a ⋅ ( b ⋅ c ) = ( a ⋅ b ) ⋅ c {\displaystyle a\cdot (b\cdot c)=(a\cdot b)\cdot c} sonucunu verir. Bunun bölme işlemi için geçerli olmadığına dikkat edin, örneğin 2 = 1 / ( 1 / 2 ) ≠ ( 1 / 1 ) / 2 = 1 / 2 {\displaystyle 2=1/(1/2)\neq (1/1)/2=1/2} .

Dağıtım özelliği

Dağılım özelliği, bir sayının başka bir terimle çarpımının dağıtılabileceğini belirtir. Örneğin: a ⋅ ( b + c ) = a b + a c {\displaystyle a\cdot (b+c)=ab+ac} . (Bunu ilişkisel özellikler ile karıştırmayın! Örneğin, a ⋅ ( b + c ) ≠ ( a ⋅ b ) + c {\displaystyle a\cdot (b+c)\neq (a\cdot b)+c} .)

Eklemeli özdeşlik özelliği

'Özdeşlik' bir sayının kendisine eşit olması özelliğini ifade eder. Başka bir deyişle, iki sayının toplamının değişkenine eşit olması için bir işlem vardır. Toplamsal özdeşlik özelliği, herhangi bir sayı ile 0'ın toplamının o sayı olduğunu belirtir: a + 0 = a {\displaystyle a+0=a} . Bu aynı zamanda çıkarma işlemi için de geçerlidir: a - 0 = a {\displaystyle a-0=a} .

Çarpımsal özdeşlik özelliği

Çarpımsal özdeşlik özelliği, herhangi bir sayı ile 1'in çarpımının o sayı olduğunu belirtir: a ⋅ 1 = a {\displaystyle a\cdot 1=a} . Bu aynı zamanda bölme işlemi için de geçerlidir: a 1 = a {\displaystyle {\frac {a}{1}}=a} .

Eklemeli ters özellik

Toplamsal ters özelliği, toplamsal özdeşlik özelliğinin tersi gibidir. Bir işlem bir sayı ile tersinin toplamı olduğunda ve 0'a eşit olduğunda, bu işlem geçerli bir cebirsel işlemdir. Cebirsel olarak şu şekilde ifade edilir: a - a = 0 {\displaystyle a-a=0} . 1'in toplamsal tersi (-1)'dir.

Çarpımsal ters alma özelliği

Çarpımsal ters alma özelliği, bir işlem bir sayı ile onun tersinin çarpımı olduğunda ve 1'e eşit olduğunda, bu işlemin geçerli bir cebirsel işlem olmasını gerektirir. Cebirsel olarak şu şekilde ifade edilir: a a = 1 {\displaystyle {\frac {a}{a}}=1} . 2'nin çarpımsal tersi 1/2'dir.

İleri Cebir

"Temel cebir" veya temel cebire ek olarak, kolejlerde ve üniversitelerde öğretilen soyut cebir, lineer cebir ve evrensel cebir gibi ileri cebir türleri de vardır. Bu, aynı anda birçok doğrusal denklemi çözmek için bir matrisin nasıl kullanılacağını içerir. Soyut cebir, sayıların ötesine geçerek sayı gruplarıyla daha soyut olan denklemlerde bulunan şeylerin incelenmesidir.

Birçok matematik problemi fizik ve mühendislikle ilgilidir. Bu fizik problemlerinin çoğunda zaman bir değişkendir. Cebirdeki temel fikirleri kullanmak, bir matematik problemini en basit haline indirgemeye yardımcı olarak zor problemleri çözmeyi kolaylaştırabilir. Enerji e, kuvvet f, kütle m, ivme a ve ışık hızı bazen c'dir. Bu, f = ma ve e=mc^2 gibi bazı ünlü denklemlerde kullanılır (son denklemi bulmak için cebirin ötesinde daha karmaşık matematik gerekmesine rağmen).

İlgili sayfalar

• Matematik konularının listesi
• Operasyon Sırası
• Parabol
• Bilgisayar Cebir Sistemi