Eşitsizlik

Eşitsizlik, bir nesnenin

diğerinden küçüktür (a < b {\displaystyle \ a<b} $\ a<b$ a'nın b'den küçük olduğu anlamına gelir)
diğerinden daha büyük (a > b {\displaystyle \ a>b} $\ a>b$ a'nın b'den daha büyük olduğu anlamına gelir)
diğerinden küçük değil (a ≥ b {\displaystyle a\geq b} $a\geq b$ a'nın b'den küçük olmadığı, yani ya daha büyük ya da b'ye eşit olduğu anlamına gelir)
diğerinden büyük değil (a ≤ b {\displaystyle a\leq b} $a\leq b$ a'nın b'den büyük olmadığı veya b'den küçük veya eşit olduğu anlamına gelir)

Eşitsizlik bazen bir ifadenin diğerinden daha küçük, daha büyük, daha küçük olmayan veya daha büyük olmayan bir ifadeyi adlandırmak için kullanılır.

Eşitsizliklerle çalışmak

Matematikte eşitsizlik, iki çözümün veya cevabın büyüktür veya küçüktür ile karşılaştırılmasıdır. Karşılaştırılan iki ya da daha fazla çözümün eşit miktarda olmadığı durumdur. Bir eşitsizliği çözmek, onun çözümlerini bulmak anlamına gelir. Bir değişkenin yerine bir sayı koyduğunuzda ve ifade doğru olduğunda, bu bir çözümdür. Bir değişkenin yerine bir sayı koyduğunuzda ve ifade doğru olmadığında, sayı ifadenin çözümü değildir.

Eşitsizlik, verilen bir değişkene bir çözüm bulmaktır. Bir kümenin göreli sırasını bulmaktır. Eşitsizliğin birçok çözümü vardır ancak gerçek çözümleri bulmanız gerekir. Eşitsizlik gerçek sayıları çözmektir. Eşitsizliği okumanın doğru yolu soldan sağa doğrudur, tıpkı diğer denklemler gibi, ancak tek fark her denklem için farklı kurallara sahip olmalarıdır.

Örneğin, x+4>12, burada x gerçek bir sayıdır. Öncelikle, bir kişinin x'i bulması ve bunun bir çözüm olup olmadığını bilmesi gerekir. Cevap x>8 olacaktır ve bu doğru bir ifadedir. Bu ifade, x'in reel sayılar kümesi içindeki konumuyla ilgilidir. Sayı doğrusu, diğer tüm reel sayılara göre konumu göstermenin bir yoludur. (Bkz. Şekil Eşitsizlik 1)

Eşitsizlik 1 Bu, x+4>12 denkleminin çözümüdür

Farklı türde eşitsizlikler

Beş farklı eşitsizlik türü vardır:

Bunlardan ilki, ifadeleri ya daha az ya da eşit, daha az ya da daha büyük ya da eşit, daha büyük ile farklılaştıran bir eşitsizlik olan doğrusal eşitsizliklerdir. Eşitsizliği eşittir ilişkisi ile değiştirirsek, sonuç doğrusal bir denklem olacaktır.
İkincisi, eşitsizlikleri karşılamak için çözüm kümelerinde bir sayıya sahip olmanız gereken eşitsizliklerin kombinasyonlarıdır, böylece eşitsizlikleri karşılayan sayılar iki çözüm kümesinin kesişimindeki değerler olacaktır.
Üçüncüsü, mutlak değerleri içeren eşitsizliklerdir; bu da değerlerin mutlak değerleri içeren eşitsizliklerin kombinasyonları olarak yeniden ifade edilebileceği anlamına gelir.
Dördüncüsü polinom eşitsizlikleri olarak adlandırılır, sürekli olduğu anlamına gelir, grafiklerinde herhangi bir atlama veya kırılma olmadığı anlamına gelir.
Sonuncu ama en az değil, rasyonel eşitsizlikler, yani bir polinomun bir polinoma bölünmüş halidir. Başka bir deyişle, rasyonel fonksiyon grafiklerinde herhangi bir kırılma veya paydanın sıfırlarında temsil yoktur.

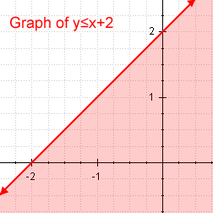
Doğrusal Eşitsizlik Doğrusal eşitsizlik örneği

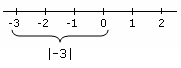
mutlak değer Mutlak değeri gösteren örnek

Eşitsizlikleri çözmenin dört yolu

İkinci dereceden denklemleri çözmenin dört yolu vardır:

Birinci kural, her iki tarafta da aynı sayıyı toplamanız veya çıkarmanız gerektiğidir.
İkinci kural, kenarları kaydırmanız ve eşitsizliğin işaretinin konumunu değiştirmeniz gerektiğidir.
Üç numaralı kural, çarpmanız gerektiğidir.
Dördüncü kural, aynı pozitif veya negatif sayıyı her iki tarafa da bölmektir. Ancak, bunları yalnızca kolay eşitsizlik problemlerinde kullanabilirsiniz.

Ayrıca, bir eşitsizliği çözmek için iki adım gerekecektir. Bunlardan ilki, toplama veya çıkarmanın tersini kullanarak sadeleştirmektir. İkincisi ise çarpma veya bölmenin karşılığını kullanarak daha fazla sadeleştirme yapmaktır. Bir eşitsizliği negatif bir sayı ile çarparken veya bölerken, eşitsizlik sembolünü çevirmeyi unutmayın.

Eşitsizliklerin eklenmesine bir örnek.

Eşitsizliğin çarpımına örnek

Eşitsizliklerin nasıl çözüleceğine dair örnekler

Eşitsizlik, iki değerin eşit ve farklı olmadığını açıklayan matematiksel bir ifadedir. Ab denklemi a'nın b'ye eşit olmadığı anlamına gelir. Eşitsizlik herhangi bir denklemle aynıdır ancak tek fark eşitsizlikte eşittir işareti kullanılmaz, bunun yerine semboller kullanılır. Eşitsizlik b>a, b'nin a'dan büyük olduğunu gösterir. Hız sınırları, işaret ve diğerleri bunları ifade etmek için eşitsizliği kullanır.

Bir eşitsizliği çözerken kişinin doğru bir ifadeye sahip olması gerekir. Her iki tarafında da negatif sayı olan bir eşitsizliği böldüğünüzde veya çarptığınızda ifade yanlıştır. Negatif bir sayı ile ifadeyi doğru hale getirmek için sembolü ters çevirmeniz gerekir. Bir sayı pozitif bir sayı olduğunda sembolü tersine çevirmeniz gerekmez. Eşitsizlik, doğru bir ifade oluşturmakla ilgilidir.

Örneğin, -6y<-12 şeklinde doğru bir ifade ile başlayın. Her iki taraf da -6 ile bölündüğünde sonuç y<2 olacaktır. Bu ifadede doğru bir ifadeye sahip olmak için sembolün ters çevrilmesi gerekir, y>2 doğru cevaptır. Sayı doğrusunda (bkz. şekil Eşitsizlik 2), kapalı gölgeli bir daire çözüm kümesine dahil olduğunu gösterir. Açık bir daire ise çözüm kümesine dahil olmadığını gösterir.

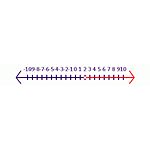
Eşitsizlik 2 -6y<-12 denkleminin çözümü

İlgili sayfalar

Eşitlik (matematik)
Denklem

Sorular ve Yanıtlar

S: "a < b" ne anlama gelir?

C: a'nın b'den küçük olduğu anlamına gelir.

S: "a > b" ne anlama gelir?

C: a'nın b'den büyük olduğu anlamına gelir.

S: "a ≥ b" ne anlama gelir?

C: a'nın b'den küçük olmadığı, yani ya b'den büyük ya da b'ye eşit olduğu anlamına gelir.

S: "a ≤ b" ne anlama gelir?

C: a'nın b'den büyük olmadığı ya da b'den küçük veya eşit olduğu anlamına gelir.

S: Eşitsizlik matematikte nasıl kullanılabilir?

C: Eşitsizlik, bir ifadenin diğerinden daha küçük, daha büyük, daha küçük olmayan veya daha büyük olmayan bir ifadeyi adlandırmak için kullanılabilir.