Temel cebir

Temel cebir, öğrencilere öğretilen en temel cebir şeklidir. Genellikle aritmetikten sonra öğrencilere öğretilen bir sonraki matematik alanlarından biridir. Aritmetikte sadece sayılar ve +, -, × ve ÷ gibi operatörler kullanılırken; cebirde değişkenler (a, x, y gibi) sayıları temsil etmek için kullanılır. Bu yararlıdır çünkü:

İnsanların "bilinmeyen" sayılarla ilgili problemleri çözmelerini sağlar. Bu, denklemleri ve bunların nasıl çözüleceğini öğrenmek anlamına gelir (örneğin, "3 x + 1 = 10 {\displaystyle 3x+1=10} $3x+1=10$ olan bir x sayısı bulun").
Aritmetik kurallarının genelleştirilmesini sağlar. Bazı öğrenciler 3 + 4 = 4 + 3 {\displaystyle 3+4=4+3} olduğunu anlarken $3+4=4+3$ tüm a ve b için a + b = b + a {\displaystyle a+b=b+a} olduğunu kanıtlamaya yardımcı olur. Bu, cebiri soyutlamayı öğrenmek için iyi bir adım haline getirir (birçok örnekten genel fikirleri öğrenmek).
İnsanların işlevsel ilişkileri (bazen neden ve sonuç olarak da adlandırılır) anlamalarına ve oluşturmalarına yardımcı olur. Bunun bir örneği "x bilet satılırsa, kar 3 x - 10 {\displaystyle 3x-10} $3x-10$ dolar olacaktır".

Bu üçü temel cebirin ana hatlarını oluşturur. Temel cebir genellikle bilim, iş ve inşaat gibi diğer birçok konuda kullanılır. Çok daha ileri bir konu olan soyut cebir genellikle üniversitenin sonlarına doğru öğretilir.

Basit cebir problemleri

Bir denklemde bilinmeyen sadece bir sayı varsa, bazen çözülmesi kolaydır. Bilinmeyen sayı "x" olarak adlandırılır:

2 x + 4 = 12. {\displaystyle 2x+4=12.\,} $2x+4=12.\,$

Tek bilinmeyenli basit bir denklemi çözmek için bilinmeyen miktarı (x) denklemin bir tarafına koymak amacıyla denklemin her iki tarafını aynı sayı ile toplayın, çıkarın, çarpın veya bölün. x bir tarafta tek başına olduğunda, denklemin diğer tarafındaki miktarı belirlemek için aritmetiği kullanın. Örneğin, yukarıdaki denklemde her iki taraftan 4 çıkararak:

2 x + 4 - 4 = 12 - 4 {\displaystyle 2x+4-4=12-4\,} $2x+4-4=12-4\,$

alıyorum:

2 x = 8 {\displaystyle 2x=8\,} $2x=8\,$

Her iki tarafı da 2'ye bölmek:

2 x 2 = 8 2 {\displaystyle {\frac {2x}{2}}={\frac {8}{2}}\,} ${\frac {2x}{2}}={\frac {8}{2}}\,$

alıyorum:

x = 4. {\displaystyle x=4.\,} $x=4.\,$

Bu denklemi bir tahterevalli veya denge olarak düşünmek yardımcı olabilir, bir tarafa ne yaparsanız diğer tarafa da onu yapmanız gerekir ve asıl amacınız x'i tek başına elde etmektir.

Tanımlar

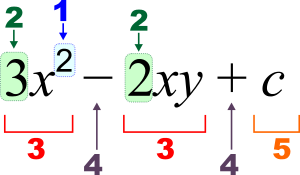
3 x 2 - 2 x y + c {\displaystyle 3x^{2}-2xy+c} $3x^{2}-2xy+c$ aşağıdaki bileşenlere sahiptir:

1 : Üs (kuvvet), 2 : Katsayı, 3 : terim, 4 : operatör, 5 : sabit, x , y {\displaystyle x,y} : $x,y$ değişkenler

Sorular ve Yanıtlar

S: Temel cebir nedir?

C: Temel cebir, öğrencilere öğretilen en temel cebir şeklidir. Genellikle aritmetiği takip eder ve denklemlerdeki sayıları ifade etmek için değişkenlerin (a, x, y gibi) kullanılmasını içerir.

S: Temel cebirin bazı kullanım alanları nelerdir?

C: Temel cebir bilinmeyen sayılarla ilgili problemleri çözmek, aritmetikteki kuralları genelleştirmek, fonksiyonel ilişkileri anlamak ve oluşturmak için kullanılabilir ve genellikle bilim, iş ve inşaat gibi diğer birçok konuda kullanılır.

S: Temel cebir insanların soyut fikirleri anlamasına nasıl yardımcı olur?

C: Temel cebir, tüm a ve b için a+b=b+a olduğunu kanıtlayarak insanların birçok örnekten genel fikirleri öğrenmelerine yardımcı olur.

S: Soyut cebir temel cebirden daha mı ileri düzeydedir?

C: Evet, soyut cebir genellikle üniversitenin sonlarına doğru öğretilir ve temel cebirden çok daha ileri düzeydedir.

S: Temel cebir ne tür denklemler içerir?

C: Temel Cebir, sayıları temsil eden değişkenlerin (a, x, y gibi) yanı sıra +,- ,× ,ve ÷ gibi operatörleri içeren denklemleri içerir.
3x+1=10 {\displaystyle 3x+1=10}

S: Temel cebiri anlamak diğer konulara nasıl yardımcı olabilir?

C: Temel Cebiri anlamak, insanların bilinmeyen sayılarla ilgili problemleri çözmelerine ve farklı değişkenler arasında fonksiyonel ilişkiler kurmalarına olanak tanıdığı için bilim, iş veya inşaat gibi diğer konularda yardımcı olabilir.