Olasılık
Olasılık, uygulamalı matematiğin bir parçasıdır. Şansla, olabilecek ya da olmayabilecek şeylerin incelenmesiyle ilgilidir.
Örneğin, olasılığı kullanarak, bir bozuk parayı havaya atıp yere düşmesine izin verdiğinizde, zamanın yarısında bir tarafı yukarı bakacak şekilde, yarısında ise diğer tarafı yukarı bakacak şekilde yere düşeceğini gösterebilirsiniz. Birçok madeni paranın bir yüzünde ünlü bir kişinin yüzünün resmi, diğer yüzünde ise başka bir şey vardır. Genellikle insanlar yüzün olduğu tarafa "tura", diğer tarafa ise "yazı" derler.
Bir olayın olasılığı (p) her zaman sıfır (imkansız) ile bir (kesin) arasındadır.
Bir zar atarsak (çoğul: zar), 1'e gelme şansı 1/6'dır (Bunun nedeni, bir zarda 6 sayı olmasıdır). Ayrıca, 2'ye gelme şansı da 1/6'dır. Çünkü 1, 2, 3, 4, 5 veya 6'ya gelebilir. Zarı her attığımızda, her zaman 1 ile 6 arasında bir sayıya gelecektir. 1 ile 6 arasındaki herhangi bir sayının gelme şansı 1'dir.
Olasılık matematik kullanılarak hesaplanabilir. Örneğin, altı zar atarsanız, ondan fazla bir sayı elde etme şansınız açık değildir, ancak matematik ve bilim kullanılarak anlaşılabilir.
Şansla ilgili en ilginç şeylerden biri, iki şeyin birlikte gerçekleşme olasılığını bulmak için iki olasılığı çarpmanızdır. Örneğin, iki zar atıp belirli bir kombinasyon elde etme olasılığını bilmek istediğinizi varsayalım (iki 6 veya bir 3 sonra bir 5 olabilir, sadece herhangi ikisi). 3 gelme olasılığı altıda birdir (⅙) ve 5 gelme olasılığı da altıda birdir, dolayısıyla 3 ve 5 gelme olasılığı ⅙×⅙=⅟36'dır. Bu sayı 0 ile 1 arasında bir yerde ifade edilirse, 0.027...7'ye eşittir ki bu oldukça düşüktür. Önce 3, sonra 5 ve ardından 2 alma olasılığı ⅙×⅙×⅙=⅟216 veya 0,00463 olacaktır ki bu çok daha düşük bir olasılıktır.
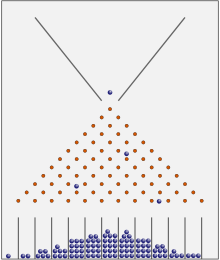
Fasulye makinesinde veya Galton kutusunda çoğu top merkeze yakın bir yerde sonlanır. Uzun vadede, normal bir dağılım göstereceklerdir
Olasılık fikirleri
Jacob Bernoulli, Pierre-Simon Laplace veya Christiaan Huygens gibi kişiler yukarıda açıklandığı gibi olasılık kelimesini kullanmışlardır. Diğer insanlar frekanslar hakkında düşündü; olasılık kavramı genellikle Frekans olasılığı olarak adlandırılır.
İlgili sayfalar
- Matematik konularının listesi
- Olasılık teorisi
| Yetki kontrolü |
|
Sorular ve Yanıtlar
S: Olasılık nedir?
C: Olasılık, uygulamalı matematiğin, olabilecek veya olmayabilecek şeylerin incelenmesiyle ilgilenen bir bölümüdür.
S: Olasılık nasıl ifade edilebilir?
C: Olasılık sıfır (imkansız) ile bir (kesin) arasında bir sayı olarak ifade edilebilir.
S: Olasılık kullanımına bir örnek nedir?
C: Olasılık kullanımına örnek olarak, bir madeni parayı havaya atıp yere düşmesine izin verdiğinizde, zamanın yarısında bir tarafı yukarı bakacak şekilde, yarısında ise diğer tarafı yukarı bakacak şekilde yere düşeceğini gösterebiliriz.
S: İki zar atma ve belirli bir kombinasyon elde etme olasılığını nasıl hesaplarsınız?
C: İki zar atma ve belirli bir kombinasyon elde etme olasılığını hesaplamak için, iki olasılığı birlikte çarparsınız. Örneğin, önce 3 sonra 5 gelme olasılığını bilmek istiyorsanız, bu 1/6 x 1/6 = 1/36 olacaktır.
S: Madeni paralar hakkında konuşurken "yazı" ne anlama gelir?
C: Madeni paralar hakkında konuşurken, "yazı" üzerinde yüz veya resim olmayan tarafı ifade eder.
S: Altı zar atıp ondan fazla bir sayı elde etme olasılığı nedir? C: Altı zar atıp ondan fazla bir sayı elde etme olasılığı matematik ve bilim kullanılarak hesaplanabilir ancak açık değildir.
S: İki olasılığı birlikte çarptığınızda ne olur?
C: İki olasılığı birlikte çarptığınızda, her iki şeyin de aynı anda gerçekleşme olasılığını hesaplamış olursunuz.
Ansiklopedi içinde ara