Daire

Daire yuvarlak, iki boyutlu bir şekildir. Dairenin kenarındaki tüm noktalar merkezden aynı uzaklıktadır.

Bir dairenin yarıçapı, dairenin merkezinden yan taraftaki bir noktaya uzanan bir çizgidir. Matematikçiler bir dairenin yarıçapının uzunluğu için r harfini kullanırlar. Bir dairenin merkezi tam ortasındaki noktadır.

Bir dairenin çapı ("boydan boya" anlamına gelir), bir taraftan diğer tarafa ve dairenin tam ortasından geçen düz bir çizgidir. Matematikçiler bu çizginin uzunluğu için d harfini kullanırlar. Bir dairenin çapı yarıçapının iki katına eşittir (d, r'nin 2 katına eşittir).

d = 2 r {\displaystyle d=2\ r} $d=2\ r$

Bir dairenin çevresi ("tüm yol boyunca" anlamına gelir), dairenin merkezinin etrafından geçen çizgidir. Matematikçiler bu çizginin uzunluğu için C harfini kullanırlar.

π sayısı (Yunanca pi harfi olarak yazılır) çok kullanışlı bir sayıdır. Çevrenin uzunluğunun çapın uzunluğuna bölümüdür (π, C'nin d'ye bölümüne eşittir). Kesir olarak π sayısı yaklaşık²² ⁄₇ veya 335/113'e (hangisi daha yakınsa) eşittir ve sayı olarak yaklaşık 3.1415926535'tir.

Bir dairenin içindeki alan, a, yarıçapın kendisi ile çarpımına ve ardından π ile çarpımına eşittir (a, π çarpı r çarpı r'ye eşittir).

Bir daire

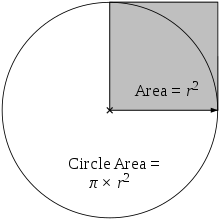
Dairenin alanı gri karenin alanının π katına eşittir.

π'nin hesaplanması

π, büyük bir daire çizilip çapı (d) ve çevresi (C) ölçülerek ölçülebilir. Bunun nedeni, bir dairenin çevresinin her zaman çapının π katı olmasıdır.

π = C d {\displaystyle \pi ={\frac {C}{d}}} $\pi ={\frac {C}{d}}$

π sadece matematiksel yöntemler kullanılarak da hesaplanabilir. π değerini hesaplamak için kullanılan yöntemlerin çoğu arzu edilen matematiksel özelliklere sahiptir. Ancak, trigonometri ve kalkülüs bilmeden anlaşılması zordur. Bununla birlikte, Gregory-Leibniz serisinin bu formu gibi bazı yöntemler oldukça basittir:

π = 4 1 - 4 3 + 4 5 - 4 7 + 4 9 - 4 11 ⋯ {\displaystyle \pi ={\frac {4}{1}}-{\frac {4}{3}}+{\frac {4}{5}}-{\frac {4}{7}}+{\frac {4}{9}}-{\frac {4}{11}}\cdots } $\pi ={\frac {4}{1}}-{\frac {4}{3}}+{\frac {4}{5}}-{\frac {4}{7}}+{\frac {4}{9}}-{\frac {4}{11}}\cdots$

Bu seriyi yazmak ve hesaplamak kolay olsa da, neden π'ye eşit olduğunu görmek kolay değildir. Anlaşılması daha kolay bir yaklaşım, orijin merkezli r yarıçaplı hayali bir daire çizmektir. O zaman, orijine olan uzaklığı d, Pisagor teoremi ile hesaplanan r'den küçük olan herhangi bir nokta (x,y) çemberin içinde olacaktır:

d = x 2 + y 2 {\displaystyle d={\sqrt {x^{2}+y^{2}}}} $d={\sqrt {x^{2}+y^{2}}}$

Dairenin içinde bir dizi nokta bulmak, dairenin A alanının tahmin edilmesini sağlar. Örneğin, büyük bir r için tam sayı koordinatları kullanarak. Bir dairenin A alanı yarıçapın karesinin π katı olduğundan, π kullanılarak yaklaşık olarak hesaplanabilir:

π = A r 2 {\displaystyle \pi ={\frac {A}{r^{2}}}} $\pi ={\frac {A}{r^{2}}}$

İlgili sayfalar

Küre

Sorular ve Yanıtlar

S: Daire nedir?

C: Daire yuvarlak, iki boyutlu bir şekildir. Dairenin kenarındaki tüm noktalar merkezden aynı uzaklıktadır.

S: Matematikçiler bir dairenin yarıçapının uzunluğunu ifade etmek için ne kullanırlar?

C: Matematikçiler bir dairenin yarıçapının uzunluğu için r harfini kullanırlar.

S: Çemberlerde O olarak ne yazılır?

C: Bir dairenin merkezi genellikle O olarak yazılır.

S: Bir dairenin çapı ne kadar uzunluktadır?

C: Bir dairenin çapı ("boydan boya" anlamına gelir), bir taraftan diğer tarafa ve dairenin tam ortasından geçen düz bir çizgidir. Yarıçapının iki katına eşittir (d, r'nin 2 katına eşittir).

S: Matematikçiler çevreyi temsil etmek için hangi harfi kullanırlar?

C: Matematikçiler çevre için "her taraf" anlamına gelen C harfini kullanırlar.

S: Bir dairenin içindeki alanı nasıl hesaplayabiliriz?

C: Bir dairenin içindeki alan, A, yarıçapının kendisi ile çarpılması ve ardından ً ile çarpılmasıyla hesaplanabilir (A, ً çarpı r çarpı r'ye eşittir).