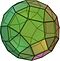
Arşimet katı

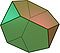
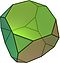
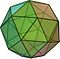
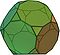
Geometride Arşimet katı, çokgenlerden oluşan dışbükey bir şekildir. Aşağıdaki özelliklere sahip bir çokyüzlüdür:

Her yüz düzenli bir çokgenden oluşur
Şeklin tüm köşeleri aynı görünüyor
Bu şekil ne platonik bir katı, ne bir prizma ne de bir antiprizmadır.

Sayım şekline bağlı olarak, bu tür on üç veya on beş şekil vardır. Bu şekillerden ikisinin, döndürme kullanılarak uyumlu hale getirilemeyen iki versiyonu vardır. Arşimet katıları, isimlerini muhtemelen MÖ 3. yüzyılda onları keşfeden Antik Yunan matematikçi Arşimet'ten almıştır. Arşimet'in yazıları kaybolmuştur, ancak İskenderiyeli Pappus 4. yüzyılda bunları özetlemiştir. Rönesans döneminde sanatçılar ve matematikçiler saf formlara değer vermiş ve tüm bu formları yeniden keşfetmişlerdir. Johannes Kepler muhtemelen bu arayışı 1620 civarında tamamlamıştır.

Bir Arşimet katı oluşturmak için en az iki farklı çokgen gerekir.

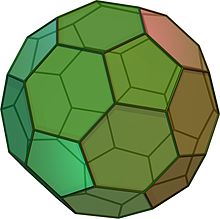
Kesik bir ikosahedron futbol topuna benzer. 12 eşkenar beşgen ve 20 düzgün altıgenden oluşur. 60 köşesi ve 90 kenarı vardır. Bir Arşimet katıdır

Özellikler

Arşimet katıları düzenli çokgenlerden oluşur, bu nedenle tüm kenarlar aynı uzunluğa sahiptir.
Tüm Arşimet katıları, platonik katıların "kenarları kesilerek" platonik katılardan üretilebilir.
Bir köşede buluşan çokgenlerin türü ("tepe noktası") hem Arşimet hem de platonik katıları karakterize eder

Platonik katılar ile ilişki

Platonik katılar, yapıları için bir dizi kural izlenerek Arşimet katılarına dönüştürülebilir.

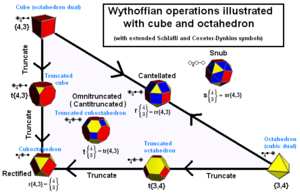
Arşimet katıları bir kaleydoskoptaki jeneratör konumları olarak inşa edilebilir

Arşimet katılarının listesi

Aşağıda tüm Arşimet katılarının bir listesi verilmiştir

Resim	İsim	Yüzler	Tip	Kenarlar	Köşeler
	Kesik tetrahedron	8	4 üçgen 4 altıgen	18	12
	Cuboctahedron	14	8 üçgen 6 kare	24	12
	Kesilmiş küp	14	8 üçgen 6 sekizgen	36	24
	Kesik oktahedron	14	6 kare 8 altıgen	36	24
	Rhombicuboctahedron	26	8 üçgen 18 kare	48	24
	Kesik küboktahedron	26	12 kare 8 altıgen 6 sekizgen	72	48
	Snub küp (2 aynalı versiyon)	38	32 üçgen 6 kare	60	24
	Icosidodecahedron	32	20 üçgen 12 beşgen	60	30
	Kesik dodekahedron	32	20 üçgen 12 dekagon	90	60
	Kesik ikosahedron	32	12 beşgen 20 altıgen	90	60
	Rhombicosidodecahedron	62	20 üçgen30 kare12 beşgen	120	60
	Kesik ikosidodekahedron	62	30 kare 20 altıgen 12 dekagon	180	120
	Snub dodecahedron (2 aynalı versiyon)	92	80 üçgen 12 beşgen	150	60

Sorular ve Yanıtlar

S: Arşimet katı nedir?

C: Arşimet katı, her bir yüzün düzgün bir çokgen olması, tüm köşelerin aynı görünmesi ve platonik katı, prizma veya antiprizma olmaması özelliklerine sahip çokgenlerden oluşan dışbükey bir şekildir.

S: Kaç tane Arşimet katı vardır?

C: Nasıl sayıldıklarına bağlı olarak, on üç ya da on beş Arşimet katı vardır.

S: Arşimet katılarını kim keşfetti?

C: Arşimet katıları, isimlerini muhtemelen MÖ 3. yüzyılda keşfeden Antik Yunan matematikçi Arşimet'ten almıştır.

S: İskenderiyeli Pappus Arşimet'in yazılarıyla ne yaptı?

C: İskenderiyeli Pappus, 4. yüzyılda Arşimet'in Arşimet katıları hakkındaki yazılarını özetlemiştir.

S: Rönesans döneminde sanatçılar ve matematikçiler Arşimet katılarını neden yeniden keşfettiler?

C: Rönesans döneminde sanatçılar ve matematikçiler saf formlara değer verdiler ve Arşimet katıları saf formlar olarak kabul edildi.

S: Johannes Kepler tüm Arşimet katılarını araştırmayı ne zaman tamamladı?

C: Johannes Kepler muhtemelen 1620 civarında tüm Arşimet katılarını araştırmayı tamamladı.

S: Bir Arşimet katı oluşturmak için ne gereklidir?

C: Bir Arşimet katı oluşturmak için en az iki farklı çokgen gerekir.