Işık saati

Işık saati, Özel göreliliğin temel bir özelliğini göstermenin basit bir yoludur. Bir saat, uzaktaki bir aynadan bir ışık parıltısı yansıtarak ve geri dönüşünü başka bir ışık parıltısını tetiklemek için kullanarak, bu arada yol boyunca kaç parıltı meydana geldiğini sayarak çalışmak üzere tasarlanmıştır. Böyle bir saatle tepelerinde uçan bir uzay gemisini izleyen Dünya'daki insanların saatin nispeten yavaş işlediğini göreceklerini göstermek kolaydır. Bu etkiye zaman genişlemesi denir.

Işık saatini incelemeden önce, başka bir görelilik türünü ele alalım. Birisinin büyük bir kargo jetinin ambarında basketbol topu oynadığını düşünün. Basketbol oyuncusu jet uçağıyla aynı yönde hareket ediyor. Uçaktaki diğer insanlar onun bir top sürerken bir ya da iki metre hareket ettiğini görürler. Topun ilk kez sekmesi ile ikinci kez sekmesi arasında yaklaşık bir saniye geçmiştir. Ancak ilk sıçrama gerçekleştiğinde basketbol topu Cebelitarık'ın üzerindeydi ve ikinci sıçrama gerçekleştiğinde basketbol topu İspanya'ya daha yakın olan suyun üzerindeydi. Yani basketbol topu Dünya'ya göre 280 metre hareket etmiştir.

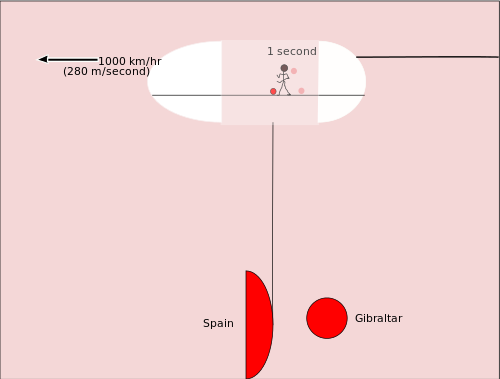
Şimdi biraz benzer bir göreli hareket sorusunu ele alalım. Bu kez Kuzey Kutbu'ndan yıldızlara bakan insanların çok hızlı bir uzay gemisi üzerlerinden geçerken ne gördüklerini ele alacağız. Uzay gemisinde zamanın ne kadar yavaşladığını hesaplamak için cebir ve Pisagor teoremini kullanabiliriz. İhtiyacımız olan diğer tek şey, mesafe, d, seyahat hızı, r ve zaman, t ile ilgili denklemdir:

d = rt

Işık hızı sabittir, bu nedenle bu değeri iki probleme uygulayacağız. Işık hızını c olarak adlandıracağız, çünkü bilim insanları genellikle bu harfi kullanmaktadır.

Uzun bir direğin dibine bir ışık çıkışı, direğin üstüne bir ayna ve direğin dibine elektronik bir ışık detektörü yerleştirilerek bir saat yapılır. Saat, direğin dibinden direğin tepesine bir ışık yanıp sönmesi gönderen ve buradan da direğin dibine geri yansıyan bir anahtarın kısa süreliğine kapatılmasıyla başlatılır. Direğin dibindeki ışık detektörü ışığın yanıp söndüğünü gördüğünde iki şey yapar. Kendisine bağlı olan sayaca bir tane ekler ve aynaya başka bir ışık yanıp sönmesi gönderir. Bu ışık yanıp sönmesi aşağıya geri döndüğünde, sayım ikiye dönüşür ve başka bir ışık yanıp sönmesi başlatılır. Işık çok hızlı hareket ettiğinden (saniyede 300.000 kilometre), sıradan bir saat tarafından ölçülen her saniye için ışık saati çok fazla sayıda "tik" atacaktır.

Matematiği kolaylaştırmak için, direğin yarım kilometre uzunluğunda olduğunu söyleyeceğiz. Yani Kuzey Kutbu'ndaki büyük teleskobun yanına inşa edilen ışık saatinin yanında duruyorsak, ışık saatinin her "tik "inde ışığın bir kilometre yol kat ettiğini göreceğiz. Katedilen mesafe, d, hızın zamanla çarpımına eşit olduğundan ve söz konusu hız c olduğundan, denklemi elde ederiz:

d = ct

ve bu denklemi t için çözerek her bir "tik "in saniye cinsinden ne kadar uzun olduğunu öğrenebiliriz.

1 km = 300.000 km/saniye * t saniye

t saniye = 1 km/300.000 (km/saniye) = 1/300.000 saniye = 0,00000333...3 saniye

Başka bir deyişle, ışık saatinin her bir "tik "i 0.00000333...3 saniye sürecektir.

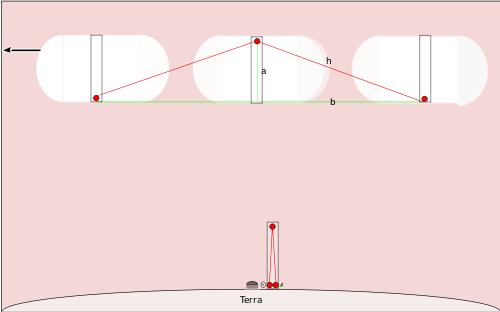
Eğer bir uzay gemisi Kuzey Kutbu'nun üzerinden ışık hızının büyük bir kısmıyla geçen düz bir çizgi üzerinde uçuyor olsaydı ve benzer bir saate sahip olsaydı, geçişini izleyen insanlar kutbun tepesindeki aynanın doğrudan ışık yayanın üzerinden hareket ettiğini göreceklerdi, böylece ışık diyagramda h ile işaretlenmiş çizgi boyunca ilerleyecek ve sonra diğer hipotenüsü takip ederek kutbun tabanına geri dönecekti - uzay gemisi çok hızlı hareket ettiği için şimdiye kadar bir miktar mesafe kat etmiş olacaktı. Dünya'daki insanlara göre bir tikin ne kadar zaman alacağını hesaplayabiliriz. Uzay gemisinin kutbunun a uzunluğunda olduğunu biliyoruz, çünkü Kuzey Kutbu'ndaki insanların kullandığı saatle aynı türden bir saat. Uzay gemisindeki saatin bir tik tak yapması için gereken süre olan t' değerini bulmak istiyoruz.

Uzay gemisinin, ışığın yanıp sönmesi aynaya doğru ilerlerken 1/2 r t' ve ışığın yanıp sönmesi direğin tabanına doğru inerken bir başka 1/2 r t' yol alacağını biliyoruz. Bu hesaplama bize grafikteki b çizgisinin uzunluğunu verir. a'yı biliyoruz, dolayısıyla Pisagor teoremiyle h'yi bulabiliriz:

h = √(a² + (rt' /2)² )

Dolayısıyla ışığın kat ettiği toplam mesafe 2 h veya d = 2 √(a² + (rt' /2)² )

Ayrıca ışık hızının, c, sabit olduğunu da biliyoruz. Kim ölçerse ölçsün, aynı hızda olduğu ortaya çıkar. Dolayısıyla, bu gerçeği kullanarak, ışık flaşının tabandan direğin tepesine gidip tekrar geri gelmesinin ne kadar sürdüğünü hesaplamanın başka bir yolunu bulabiliriz:

t' = d/c

Başka bir deyişle, d = c t' .

Yani şöyle yazabiliriz

c t' = 2 √(a² + (rt' /2)² )

veya

1/2 c t' = √(a² + (rt' /2)² )

Yukarıdaki denklemi çözmek için şunları yapmamız gerekecek:

Her iki tarafı kare
Her iki tarafı da t' ile bölün ²
Her iki tarafı da 4 ile çarpın
Her iki tarafı c'ye bölün²
Basitleştirin c² / c²
Her iki taraftan r² /c² çıkarınız
Her iki tarafın karekökünü alın
Her iki tarafı da t' ile çarpın
Her iki tarafı √(1-r² /c² ) ile bölün.

Yukarıdaki denklemi çözdüğümüzde şunu buluruz:

t' = 2a/(c√(1-r² /c² )

Kuzey Kutbu'ndaki saatin tik takları arasındaki süre 2a/c'dir, dolayısıyla şöyle yazabiliriz:

t' = t/√(1-r² /c² )

Eğer t = 1 saniye ise, uzay gemisi ışık hızının yarısı kadar bir hızla hareket ediyorsa, t' = 1,1547 saniyedir.

Çeşitli seyahat hızlarını şu adreste deneyin: http://www.1728.org/reltivty.htm

Sorular ve Yanıtlar

S: Hafif çan nedir?

C: Işık saati, özel göreliliğin temel bir özelliğini göstermek için tasarlanmış bir cihazdır. Uzaktaki bir aynadan bir ışık parlaması yansıtarak ve geri dönüşünü başka bir ışık parlamasını tetiklemek için kullanarak çalışır ve yol boyunca kaç parlama meydana geldiğini sayar.

S: Zaman genişlemesi nedir?

C: Zaman genişlemesi, Dünya'daki insanlar bir uzay gemisinin uçuşunu ışık saati aracılığıyla izlediğinde ortaya çıkan bir olgudur. Göreliliğin etkisi altında nispeten yavaş işlediğini görüyorlar.

S: Bir uzay gemisinde zamanın ne kadar yavaşladığını nasıl hesaplayabiliriz?

C: Bir uzay gemisinde zamanın ne kadar yavaşladığını hesaplamak için cebir ve Pisagor teoremini kullanabiliriz. İki problemde d = rt (mesafe eşittir hız çarpı zaman) denklemini uygulamamız ve sabit ışık hızı c'yi kullanmamız gerekiyor.

S: Işıklı saat nasıl çalışır?

C: Bir ışık saati, uzun bir çubuğun alt kısmında bir ışık kaynağı ile üst kısmında bir ayna ve alt kısmında bir elektronik dedektörden oluşur. Açıldığında, tek bir ışık parlaması aşağıdan yukarıya doğru geçer, burada alttaki dedektör tarafından algılandığında aşağıya doğru geri yansıtılır, bu da bağlı sayaca bir sayaç ekler ve tekrar yukarı doğru bir başka parlamayı tetikler. Bu işlem durdurulana veya sıfırlanana kadar devam eder.

S: Bu hesaplama için hangi denkleme ihtiyacımız var?

C: t' = 2a/(c√(1-r2/c2)) değerine ihtiyacımız var, burada t' (Kuzey Kutbu saatinin tik takları arasındaki süre) 2a/c bölü √(1-r2/c2) değerine eşittir. Eğer t = 1 saniye ise ve ışık hızının yarısıyla hareket ediyorsa, t' = 1.1547 saniyedir.

S. Pisagor teoreminin bu hesaplamayla ilişkisi nedir?

C: Pisagor teoremi, her bir tikin saniye cinsinden ne kadar sürdüğünü (d=ct) hesaplamamızı sağlayan denklemin bir parçası olan h'yi (hipotenüs) bulmamıza yardımcı olur. h'yi bildikten sonra t' değerini çözebiliriz, bu da bize Kuzey Kutbu'ndan bakan Dünya'daki insanlara ve üzerlerinden çok hızlı geçen gemideki insanlara göre her bir ilmeğin ne kadar sürdüğünü gösterir.