Olasılık yoğunluk fonksiyonu

Olasılık yoğunluk fonksiyonu, herhangi bir sürekli olasılık dağılımı için tanımlanabilen bir fonksiyondur. Olasılık yoğunluk fonksiyonunun [ a , b ] {\displaystyle [a,b]} $[a,b]$ aralığındaki integrali, verilen yoğunluğa sahip belirli bir rastgele değişkenin verilen aralıkta bulunma olasılığını verir.

Olasılık yoğunluk fonksiyonu, sürekli dağılımlarla çalışabilmek için gereklidir. Bir zar atmak, 1 6 {\displaystyle {\tfrac {1}{6}}} olasılığı ile 1 ila 6 sayılarını verecektir. ${\tfrac {1}{6}}$ Ancak bu sürekli bir fonksiyon değildir, çünkü sadece 1'den 6'ya kadar olan sayılar mümkündür. Buna karşılık, iki kişi aynı boya veya aynı ağırlığa sahip olmayacaktır. Bir olasılık yoğunluk fonksiyonu kullanarak, 180 santimetre (71 inç) ile 181 santimetre (71 inç) arasındaki veya 80 kilogram (176,4 lb) ile 81 kilogram (178,6 lb) arasındaki kişilerin olasılığını belirlemek mümkündür, ancak bu iki sınır arasında sonsuz sayıda değer vardır.

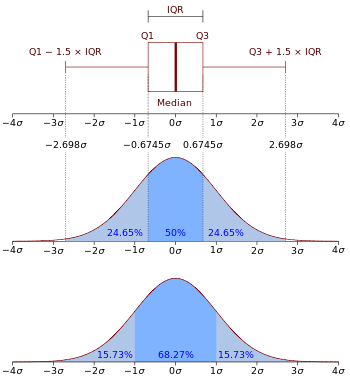
N (0, σ2 ) normal dağılımının kutu grafiği ve olasılık yoğunluk fonksiyonu.

Sorular ve Yanıtlar

S: Olasılık yoğunluk fonksiyonu nedir?

C: Olasılık yoğunluk fonksiyonu, herhangi bir sürekli olasılık dağılımını karakterize eden bir fonksiyondur.

S: Bir X rastgele değişkeninin olasılık yoğunluk fonksiyonu nasıl yazılır?

C: X'in olasılık yoğunluk fonksiyonu bazen f_X(x) olarak yazılır.

S: Olasılık yoğunluk fonksiyonunun integrali neyi temsil eder?

C: Olasılık yoğunluk fonksiyonunun integrali, verilen yoğunluğa sahip belirli bir rastgele değişkenin verilen bir aralıkta yer alma olasılığını temsil eder.

S: Olasılık yoğunluk fonksiyonu etki alanı boyunca her zaman negatif değil midir?

C: Evet, tanım gereği, olasılık yoğunluk fonksiyonu etki alanı boyunca negatif değildir.

S: Bir aralık üzerinde integral almanın toplamı 1 midir?

C: Evet, bir aralık üzerinde integral almanın toplamı 1'dir.

S: Bir Olasılık Yoğunluk Fonksiyonu ne tür bir dağılımı karakterize eder?

C: Bir Olasılık Yoğunluk Fonksiyonu herhangi bir sürekli olasılık dağılımını karakterize eder.