Boyutlar
Boyutlar dünyamızı görme, ölçme ve deneyimleme biçimimizdir. Yukarı ve aşağı, sağdan sola, arkadan öne, sıcak ve soğuk, ne kadar ağır ve ne kadar uzun gibi matematik ve fizikten daha ileri kavramları kullanarak. Bir boyutu tanımlamanın bir yolu, serbestlik derecelerine veya bir nesnenin belirli bir alanda hareket edebilme şekline bakmaktır. Boyut teriminin kullanıldığı farklı kavramlar veya yollar olduğu gibi farklı tanımlar da vardır. Tüm kavramları karşılayabilecek bir tanım yoktur.
Bir vektör uzayında (bir vektör açık uçlu bir çizgidir) bir boyut, vektörlerin veya çizgilerin yönlerinin kardinalitesine veya sayısına eşittir. Aynı zamanda o uzayın en büyük düz çizgi yönleri grubunun sayısına da eşittir. Günlük yaşamdaki "normal" nesneler, genellikle uzunluk, genişlik ve derinlik olarak adlandırılan üç boyutla belirtilir. Matematikçiler bu kavramı Öklid uzayı olarak adlandırırlar.
Boyutlar, konumu ölçmek için de kullanılabilir. Bir başlangıç yerinden bir konuma olan mesafe uzunluk, genişlik ve yükseklik yönlerinde ölçülebilir. Bu mesafeler konumun bir ölçüsüdür.
Bazen dördüncü (4D) boyut olan zaman, bir olayın zaman ve uzaydaki konumunu göstermek için kullanılır.
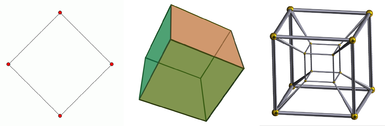
Soldan sağa, kare, küp ve tesseract. Kare 2 boyutlu bir nesne, küp 3 boyutlu bir nesne ve tesseract 4 boyutlu bir nesnedir. 1 boyutlu bir nesne sadece bir çizgidir. İki boyutlu bir ekranda görüntülendiği için küpün bir izdüşümü verilmiştir. Aynı şey tesseract için de geçerlidir ve bu da üç boyutlu uzayda bile yalnızca bir izdüşüm olarak gösterilebilir.

İlk dört uzamsal boyutun bir diyagramı.
Diğer Boyutlar
Modern bilimde insanlar başka boyutlar kullanırlar. Sıcaklık ve ağırlık gibi boyutlar, daha az basit alanlarda bir şeyin konumunu göstermek için kullanılabilir. Bilim insanları bu boyutları boyutsal analiz ile inceler.
Matematikçiler de boyutları kullanır. Matematikte boyutlar daha geneldir. Matematikteki boyutlar dünyadaki şeyleri ölçmeyebilir. Matematikte boyutlarla aritmetik yapmanın kuralları normal aritmetik kurallarından farklı olabilir.
Boyutlar ve vektörler
Vektörler mesafeleri ve yönleri göstermek için kullanılır. Vektörler genellikle mühendislik ve fen bilimlerinde ve bazen de matematikte kullanılır.
Vektör, sayılardan oluşan bir listedir. Her boyut için bir sayı vardır. Vektörler için aritmetik kurallar vardır.
Örneğin, Jane Sally'nin konumunu bilmek isterse, Sally Jane'e konumu göstermek için bir vektör verebilir. Eğer Jane ve Sally dünyada iseler, üç boyut vardır. Bu nedenle, Sally Jane'e konumunu göstermek için üç sayıdan oluşan bir liste verir. Sally'nin Jane'e verdiği vektördeki üç sayı şunlar olabilir:
- Sally'nin Jane'in kuzeyine olan uzaklığı
- Sally'nin Jane'in doğusuna olan uzaklığı
- Sally'nin Jane'den yüksekliği
Sorular ve Yanıtlar
S: Boyut nedir?
C: Boyut, yukarı ve aşağı, sağdan sola, arkadan öne, sıcak ve soğuk, ne kadar ağır ve ne kadar uzun gibi kavramları kullanarak dünyayı ölçmenin, görmenin ve deneyimlemenin bir yoludur. Serbestlik derecesi veya bir nesnenin belirli bir alanda hareket edebilme şekli olarak da tanımlanabilir.
S: Matematikçiler Öklid uzayını nasıl tanımlar?
C: Matematikçiler Öklid uzayını genellikle uzunluk, genişlik ve derinlik olarak adlandırılan üç boyutla tanımlarlar.
S: Bir vektör uzayındaki vektör sayısı nedir?
C: Bir vektör uzayındaki vektör sayısı, temel kümesinin kardinalitesine (veya vektör sayısına) eşittir.
S: Konumu ölçmek için kaç boyut kullanılır?
C: Pozisyonu ölçmek için üç boyut (uzunluk, genişlik ve yükseklik) kullanılır. Bazı durumlarda, bir olayın zaman ve uzaydaki konumunu göstermek için dördüncü (4D) bir boyut - zaman - kullanılabilir.
S: dim(V) ne anlama gelir?
C: Dim(V), V'nin temel kümesinin kardinalitesine (veya vektör sayısına) eşit olan veya sahip olduğu düz çizgi yönlerinin sayısına eşit olan boyutunu ifade eder.
S: Boyutlarla ilgili tüm kavramları karşılayan tek bir tanım var mıdır?
C: Hayır, boyutlarla ilgili tüm kavramları karşılayabilecek tek bir tanım yoktur.
Ansiklopedi içinde ara