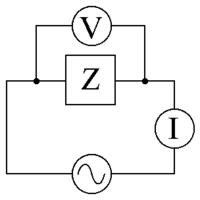
Elektriksel empedans
Elektriksel empedans, bir devrenin akım veya voltaj değişimine gösterdiği karşıtlık miktarıdır.
Bir empedans yazmanın iki ana yolu vardır: (bkz. 2. şekil, "karmaşık empedans düzlemi")
- "R" direnci (gerçek kısım) ve "X" reaktansı (hayali kısım) ile, örneğin Z = 1 + 1 j {\displaystyle Z=1+1j}
- bir büyüklük ve bir faz ile (boyut | Z | {\displaystyle \left\vert Z\right\vert }
ve açı ∠ θ {\displaystyle \angle \theta } 
), örneğin Z = 1.4 ∠ 45 ∘ {\displaystyle Z=1.4\angle 45^{\circ }} 
(45 derecede 1,4 ohm)
Empedans ve direnç oldukça benzerdir:
Direnç söz konusu olduğunda, bir direnç içinden geçen herhangi bir akıma direnç gösterir. Direnç ne kadar yüksek olursa, belirli bir akımı elde etmek için gereken voltaj da o kadar yüksek olur. Formül şöyledir:
V = R ∗ I {\displaystyle V=R*I}
, burada V gerilim, R direnç ve I akımdır.
Empedans durumunda, bir indüktör akımdaki değişikliklere direnç gösterir ve kapasitör voltajdaki değişikliklere direnç gösterir.
Direnç ve empedans arasındaki temel fark "değişim" kelimesidir, değişim oranı empedansı etkiler. Genellikle "değişim" bir frekans olarak ifade edilir, akım veya voltajın saniyede kaç kez yön değiştirdiği. Formüller şöyledir:
İndüktör için: Z = j 2 π f L {\displaystyle Z=j2\pi fL\,} 
Kondansatör için: Z = 1 j 2 π f C {\displaystyle Z={\frac {1}{j2\pi fC}} 
Burada Z empedansın sembolüdür, j hayali sayıdır - 1 {\displaystyle {\sqrt {-1}} 
, π {\displaystyle \pi } 
pi sabiti, f frekans, L endüktans ve C kapasitanstır. Direnç ve empedans için birimler aynıdır, ohm sembolü Ω {\displaystyle \Omega } 
(büyük omega).
Yukarıdaki formüllerde belirtildiği gibi, empedans frekansa bağlı olarak değişir, örneğin, sıfır Hertz'de veya DC'de, indüktörün empedansı sıfırdır, kısa devre ile aynıdır ve kapasitörün empedansı sonsuzdur, açık devre ile aynıdır. Çoğu sinyal, çeşitli frekanslardaki birçok sinüs dalgasının toplamıdır (daha fazla ayrıntı için fourier dönüşümüne bakın) ve her biri farklı bir empedansa maruz kalır.
Dirence benzer şekilde, empedans ne kadar yüksekse, belirli bir akım elde etmek için gereken voltaj da o kadar yüksek olur. Formül şöyledir:
V = Z ∗ I {\displaystyle V=Z*I}
, burada V gerilim, Z empedans ve I akımdır.
Fiziksel düzeyde, birçok şeyi basitleştirmek:
- Direnç, elektronların dirençlerin içindeki atomlarla çarpışmasından kaynaklanır.
- Bir kondansatördeki empedans, bir elektrik alanının yaratılmasından kaynaklanır.
- Bir indüktördeki empedans, manyetik bir alanın yaratılmasından kaynaklanır.
Direnç ve empedans arasındaki önemli bir fark, bir direncin enerjiyi dağıtması, ısınması, ancak bir indüktör ve bir kapasitörün enerjiyi depolaması ve düştüğünde bu enerjiyi kaynağa geri verebilmesidir.
Kaynak, kablo ve yükün empedansı eşit değilse, sinyalin bir kısmı kaynağa geri yansıyarak güç israfına ve parazite neden olur. Yansıma oranı şu şekilde hesaplanabilir:
Γ = Z L - Z S Z L + Z S {\displaystyle \Gamma ={Z_{L}-Z_{S} \over Z_{L}+Z_{S}}}
burada Γ {\displaystyle \Gamma } 
(büyük gama) Yansıma katsayısı, Z S {\displaystyle Z_{S}}
kaynağın empedansı, Z L {\displaystyle Z_{L}}
yükün empedansıdır.
Bir dalgaya sahip olabilen her ortamın bir dalga empedansı vardır, boş uzay bile (ışık bir elektromanyetik dalgadır ve uzayda hareket edebilir) yaklaşık 377 Ω {\displaystyle \Omega } empedansa sahiptir. .
Karmaşık empedans düzleminin grafiksel gösterimi
V {\displaystyle \scriptstyle V} gerilimi uygulayan bir AC kaynağı 
, bir Z empedansı boyunca {\displaystyle \scriptstyle Z} 
, bir akım I {\displaystyle \scriptstyle I}
sürmektedir.
Bir sinyal, empedansın değiştiği yerde kısmen geri yansıtılır.
Aşama
Bir direnç karşısında, hem voltaj hem de akım aynı anda yukarı ve aşağı gider, fazda oldukları söylenir, ancak bir empedans ile durum farklıdır, voltaj bir kapasitörde akımın 1/4 dalga boyu gerisine ve bir indüktörde ileriye kaydırılır.
1/4 dalga boyu genellikle hayali "j" sayısı ile gösterilir ve bu da 90 derecelik bir kaymaya eşdeğerdir.
Hayali "j" sayısının kullanılması matematiği çok daha basit hale getirir, toplam empedansı dirençlerle yapıldığı gibi hesaplamaya izin verir, örneğin bir direnç artı seri olarak bir empedans R+Z'dir ve paralel olarak (R*Z)/(R+Z)'dir.
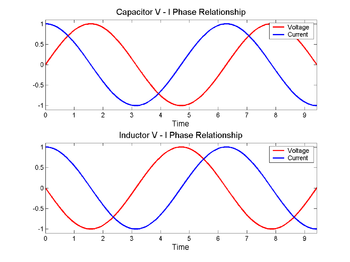
Bir kapasitörde (üstte) voltaj (kırmızı) akımdan (mavi) sonra, bir indüktörde (altta) ise önce değişir. Gerilim ve akım arasındaki faz farkı 1/4 dalga boyudur.
Sorular ve Yanıtlar
S: Elektriksel empedans nedir?
C: Elektriksel empedans, bir devrenin akım veya voltaj değişimine gösterdiği karşıtlık miktarıdır.
S: Elektriksel empedans nasıl yazılabilir?
C: Elektriksel empedans, direnç "R" (gerçek kısım) ve reaktans "X" (hayali kısım) ile birlikte bir büyüklük, faz, boyut ve açı ile yazılabilir.
S: Direnç ve empedans arasındaki fark nedir?
C: Direnç ve empedans arasındaki temel fark "değişim" kelimesidir; başka bir deyişle, değişim oranı empedansı etkiler. Direnç, içinden geçen herhangi bir akıma direnç gösterirken, bir indüktör akımdaki değişikliklere ve bir kondansatör voltajdaki değişikliklere direnç gösterir.
S: Direnç ve empedans ile ilgili bazı formüller nelerdir?
C: Direnç için V=R*I, burada V voltaj, R direnç ve I akımdır; indüktörler için Z=j2πfL; kapasitörler için Z=1/j2πfC; burada Z empedansı, j hayali sayı -1'i, π sabit pi'yi, f frekansı, L endüktansı, C kapasitansı temsil eder.
S: Direnç ve empedans için bazı fiziksel açıklamalar nelerdir?
C: Direnç, dirençlerin içindeki atomlarla çarpışan elektronlardan kaynaklanırken, bir indüktörün empedansı bir elektrik alanı yaratmaktan ve bir kapasitörün empedansı bir manyetik alan yaratmaktan gelir. Ayrıca, dirençler enerjiyi dağıtırken, indüktörler ve kapasitörler enerji depolar ve enerji azaldığında kaynağa geri gönderilebilir.
S: Yansıma katsayısı nasıl hesaplanır?
C: Yansıma katsayısı Γ=(ZL-ZS)/(ZL+ZS) kullanılarak hesaplanabilir; burada Γ (büyük gama) yansıma katsayısı anlamına gelir; ZS kaynağın empedansını temsil eder; ZL yükün empedansını temsil eder
