Fourier dönüşümü

Fourier dönüşümü, bir sinyal veya dalgayı oluşturan temel frekansları bulmak için kullanılabilen matematiksel bir fonksiyondur. Örneğin, bir akor çalındığında, akorun ses dalgası Fourier dönüşümüne sokularak akorun hangi notalardan oluştuğu bulunabilir. Bir Fourier dönüşümünün çıktısı bazen frekans spektrumu veya dağılımı olarak adlandırılır çünkü girdinin frekanslarının bir spektrumunu gösterir. Bu fonksiyon kriptografi, oşinografi, makine öğrenimi, radyoloji, kuantum fiziği, ses tasarımı ve görselleştirmede birçok kullanım alanına sahiptir.

Bir f ( x ) {\displaystyle f(x)} fonksiyonunun Fourier dönüşümü f(x) ile verilir.

F ( α ) = ∫ - ∞ + ∞ f ( x ) e - 2 π i α x d x {\displaystyle F(\alpha )=\int _{-\infty }^{+\infty }f(x)e^{-2\pi i\alpha x}dx} $F(\alpha )=\int _{-\infty }^{+\infty }f(x)e^{-2\pi i\alpha x}dx$

α {\displaystyle \alpha } $\alpha$ bir frekanstır

F ( α ) {\displaystyle F(\alpha )} $F(\alpha )$ Fourier dönüşüm fonksiyonudur ve orijinal sinyalde α {\displaystyle \alpha } $\alpha$ frekansının ne kadar yaygın olduğunu gösteren bir değer döndürür.

e - 2 π i α x {\displaystyle e^{-2\pi i\alpha x}} $e^{-2\pi i\alpha x}$ Giriş fonksiyonu f ( x ) {\displaystyle f(x)} 'in f(x) karmaşık düzlemde orijin etrafında bazı α {\displaystyle \alpha } frekanslarında sarılmasını temsil eder. $\alpha$

Ters Fourier dönüşümü şu şekilde verilir

f ( x ) = ∫ - ∞ + ∞ F ( α ) e + 2 π i x α d α {\displaystyle f(x)=\int _{-\infty }^{+\infty }F(\alpha )e^{+2\pi ix\alpha }d\alpha } $f(x)=\int _{-\infty }^{+\infty }F(\alpha )e^{+2\pi ix\alpha }d\alpha$

Fourier dönüşümü bir sinyalde hangi frekansların olduğunu gösterir. Örneğin, üç farklı müzik notası içeren bir ses dalgası düşünün: Bu ses dalgasının Fourier dönüşümünün bir grafiğini oluşturmak (frekans x ekseninde ve yoğunluk y ekseninde olacak şekilde) her frekansta müzik notalarından birine karşılık gelen bir tepe noktası gösterecektir.

Değişken genlik ve frekanslara sahip kosinüs ve sinüsleri bir araya getirerek birçok sinyal oluşturulabilir. Fourier dönüşümü, bu kosinüslerin ve sinüslerin genliklerini ve fazlarını ilgili frekanslarına karşı çizer.

Fourier dönüşümleri önemlidir çünkü birçok sinyal, frekansları ayrıldığında daha anlamlı hale gelir. Yukarıdaki ses örneğinde, sinyale zamana göre bakmak A, B ve C notalarının sinyalde olduğunu açıkça göstermez. Birçok sistem farklı frekanslara farklı şeyler yapar, bu nedenle bu tür sistemler her frekansa ne yaptıklarıyla tanımlanabilir. Bunun bir örneği yüksek frekansları bloke eden bir filtredir.

Fourier dönüşümünün hesaplanması, integral ve hayali sayıların anlaşılmasını gerektirir. Bilgisayarlar genellikle en basit sinyaller dışında her şeyin Fourier dönüşümlerini hesaplamak için kullanılır. Hızlı Fourier Dönüşümü, bilgisayarların Fourier dönüşümünü hızlı bir şekilde hesaplamak için kullandığı bir yöntemdir.

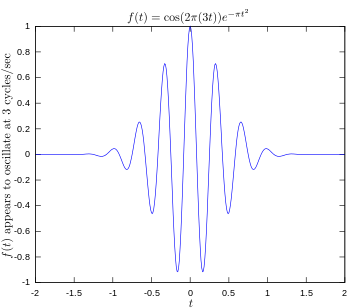
Orijinal fonksiyon 3 hertz'de salınan bir sinyali gösterir.

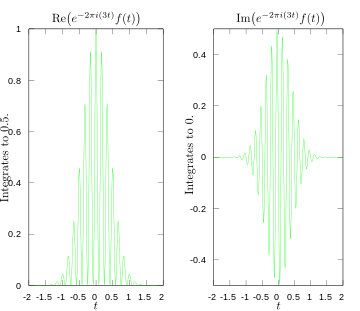
Fourier dönüşümü için 3 hertz'de integrandın reel ve imajiner kısımları

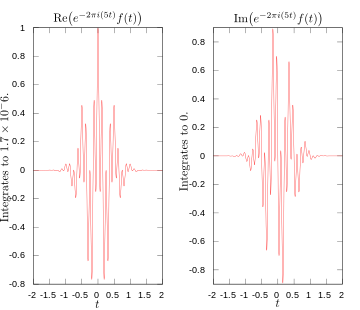
Fourier dönüşümü için 5 hertz'de integrandın reel ve imajiner kısımları

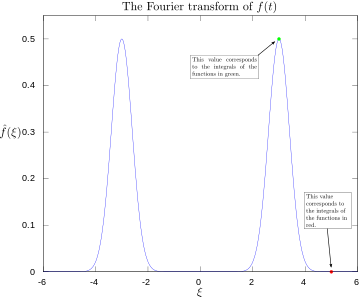
Fourier dönüşümü 3 ve 5 hertz etiketli.

Sorular ve Yanıtlar

S: Fourier dönüşümü nedir?

C: Fourier dönüşümü, bir dalganın oluştuğu temel frekansları bulmak için kullanılabilen matematiksel bir fonksiyondur. Karmaşık bir dalgayı alır ve onu oluşturan frekansları bularak bir akoru oluşturan notaları tanımlamasını sağlar.

S: Fourier dönüşümünün bazı kullanım alanları nelerdir?

C: Fourier dönüşümünün kriptografi, oşinografi, makine öğrenimi, radyoloji, kuantum fiziği, ses tasarımı ve görselleştirmede birçok kullanımı vardır.

S: Fourier dönüşümü nasıl hesaplanır?

C: Bir f(x) fonksiyonunun Fourier dönüşümü F(ב) = ∫-∞+∞f(x)e-2נiבxdx ile verilir, burada ב bir frekanstır. Bu, orijinal sinyalde ב frekansının ne kadar yaygın olduğunu temsil eden bir değer döndürür. Ters Fourier dönüşümü f(x) = ∫-∞+∞F(ב)e+2נixבdב ile verilir.

S: Bir Fourier Dönüşümünün çıktısı neye benzer?

C: Bir Fourier Dönüşümünün çıktısı, girdinin olası frekanslarının bir dağılımını gösterdiği için frekans spektrumu veya dağılımı olarak adlandırılabilir.

S: Bilgisayarlar Hızlı Fourier Dönüşümlerini nasıl hesaplar?

C: Bilgisayarlar, en basit sinyal dönüşümleri hariç tüm dönüşümleri hızlı bir şekilde hesaplamak için Hızlı Fourier Dönüşümü (FFT) adı verilen bir algoritma kullanır.

S: Sinyallere zamana göre bakmak bize neyi göstermez?

C: Sinyallere zamana göre bakmak, içlerinde hangi notaların bulunduğunu açıkça göstermez; bunun yerine frekansları ayrılıp tek tek analiz edildiğinde birçok sinyal daha anlamlı hale gelir.