Kuantum mekaniği
Kuantum Mekaniği veya QM, Evrenin atomlardan daha küçük seviyede nasıl çalıştığını açıklar. "Kuantum fiziği" veya "kuantum teorisi" olarak da adlandırılır. Kuantum Latince'de 'ne kadar' anlamına gelir ve mekanik de hareketle ilgilenen bilim dalıdır. Bir enerji kuantumu belirli bir enerji miktarıdır ve Kuantum Mekaniği bu enerjinin atom altı seviyede nasıl hareket ettiğini ve etkileştiğini açıklar.
Atomlar maddenin en küçük yapı taşları olarak kabul edilirdi, ancak modern bilim protonlar, nötronlar ve elektronlar gibi daha da küçük parçacıklar olduğunu göstermiştir. QM, atomları oluşturan parçacıkların nasıl çalıştığını açıklayan fiziğin bir parçasıdır.
QM bize elektromanyetik dalgaların (ışık gibi) nasıl çalıştığını da anlatır. Modern fizik ve kimyanın çoğu Kuantum mekaniğinin matematiksel kuralları kullanılarak tanımlanabilir ve anlaşılabilir.
Atom altı parçacıkları ve elektromanyetik dalgaları incelemek için kullanılan matematik çok karmaşıktır çünkü çok garip şekillerde hareket ederler.
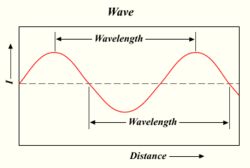
Bir ışık dalgasının dalga boyu
Dalgalar ve fotonlar
Fotonlar atomlardan, protonlardan ve elektronlardan çok daha küçük parçacıklardır; aslında hiç kütleleri yoktur. Fotonlar "paketler" ya da enerji paketleri gibidir. Mum ya da lazer gibi ışık kaynakları foton adı verilen parçalar halinde ışık yayar (ya da "yayar").
Bir lamba ne kadar çok foton yayarsa, ışık o kadar parlak olur. Işık, sudaki dalgalar veya radyo dalgaları gibi davranan bir enerji biçimidir. Bir dalganın tepesi ile bir sonraki dalganın tepesi arasındaki mesafeye 'dalga boyu' denir. Her foton, dalga boyuna bağlı olarak belirli bir miktar ya da 'kuantum' enerji taşır.
Bir ışığın rengi dalga boyuna bağlıdır. Menekşe rengi (gökkuşağının en alt veya en iç rengi) yaklaşık 400 nm ("nanometre") dalga boyuna sahiptir, bu da 0,00004 santimetre veya 0,000016 inçtir. Dalga boyları 10-400 nm olan fotonlara ultraviyole (veya UV) ışık denir. Bu ışık insan gözü tarafından görülemez. Spektrumun diğer ucunda, kırmızı ışık yaklaşık 700 nm'dir. Kızılötesi ışık yaklaşık 700 nm ila 300.000 nm arasındadır. İnsan gözü kızılötesi ışığa karşı da hassas değildir.
Dalga boyları her zaman bu kadar küçük değildir. Radyo dalgaları daha uzun dalga boylarına sahiptir. Bir FM radyo için dalga boyları birkaç metre uzunluğunda olabilir (örneğin, 99.5 FM'de yayın yapan istasyonlar yaklaşık 3 metre, yani yaklaşık 10 fit dalga boyunda radyo enerjisi yaymaktadır). Her foton, dalga boyuna bağlı olarak belirli bir enerji miktarına sahiptir. Bir fotonun dalga boyu ne kadar kısa olursa, enerjisi de o kadar büyük olur. Örneğin, morötesi bir foton kızılötesi bir fotondan daha fazla enerjiye sahiptir.
Dalga boyu ve frekans (dalganın saniyede kaç kez tepeye çıktığı) ters orantılıdır, yani daha uzun bir dalga boyu daha düşük bir frekansa sahip olacaktır ve bunun tersi de geçerlidir. Işığın rengi kızılötesi ise (frekansı kırmızı ışıktan daha düşük), her foton çarptığı şeyi ısıtabilir. Dolayısıyla, güçlü bir kızılötesi lamba (bir ısı lambası) bir kişiye doğrultulursa, o kişi birçok fotonda depolanan enerji nedeniyle ılık, hatta sıcak hissedecektir. Kızılötesi lambanın yüzeyi, ona dokunabilecek birini yakacak kadar bile ısınabilir. İnsanlar kızılötesi ışığı göremez, ancak radyasyonu ısı şeklinde hissedebiliriz. Örneğin, güneş tarafından ısıtılan tuğla bir binanın yanından geçen bir kişi, dokunmak zorunda kalmadan binadan gelen ısıyı hissedecektir.
Kuantum mekaniğinin matematiksel formülasyonları soyuttur. Dalga fonksiyonu adı verilen matematiksel bir fonksiyon, bir parçacığın konumu, momentumu ve diğer fiziksel özelliklerinin olasılık genliği (olasılık genliğinin karesi olasılıktır) hakkında bilgi sağlar. Kuantum mekaniğinin sonuçlarının çoğu klasik mekanik açısından kolayca görselleştirilemez.
Ultraviyole ışığın frekansı mor ışıktan daha yüksektir, öyle ki görünür ışık aralığında bile değildir. Ultraviyole aralığındaki her foton, cilt hücrelerine zarar verecek ve güneş yanığına neden olacak kadar çok enerjiye sahiptir. Aslında, güneş yanıklarının çoğu ısıdan kaynaklanmaz; güneşin UV ışınlarının yüksek enerjisinin cilt hücrelerinize zarar vermesinden kaynaklanır. Daha yüksek ışık frekansları (veya elektromanyetik radyasyon) bile vücudun daha derinlerine nüfuz edebilir ve daha da fazla hasara neden olabilir. X-ışınları o kadar fazla enerjiye sahiptir ki insan vücudunun derinliklerine inip hücreleri öldürebilir. İnsanlar ultraviyole ışığı veya x-ışınlarını göremez veya hissedemez. Bu tür yüksek frekanslı ışık altında kaldıklarını ancak radyasyon yanığı oluştuğunda anlayabilirler. Mikropları öldürmenin önemli olduğu alanlarda bakterileri, mantarları vb. yok etmek için genellikle ultraviyole lambalar kullanılır. X-ışınları bazen kanser hücrelerini öldürmek için kullanılır.
Kuantum mekaniği, belirli bir frekansın belirli bir enerji miktarı anlamına geldiğinin keşfedilmesiyle başlamıştır. Enerji frekans ile orantılıdır (E ∝ f). Frekans ne kadar yüksekse, bir foton o kadar fazla enerjiye sahiptir ve o kadar fazla zarar verebilir. Kuantum mekaniği daha sonra atomların iç yapısını açıklamak için geliştirildi. Kuantum mekaniği aynı zamanda bir fotonun kendi kendisiyle etkileşime girebilmesini ve klasik fizikte asla hayal edilemeyen diğer birçok şeyi de açıklar.
Soldaki siyah ultraviyole (yüksek frekans); sağdaki siyah ise kızılötesi (düşük frekans).
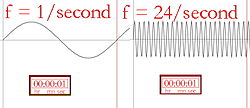
Frekansın resimli açıklaması
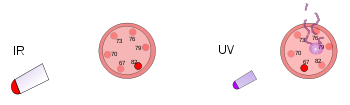
Solda, plastik bir termometre parlak bir ısı lambasının altında. Bu kızılötesi radyasyon termometreyi ısıtır ancak termometreye zarar vermez. Sağda, başka bir plastik termometreye düşük yoğunluklu ultraviyole ışık vuruyor. Bu radyasyon termometreye zarar verir ancak ısıtmaz.
Kuantizasyon
Max Planck frekans ve enerji arasındaki ilişkiyi keşfetti. Daha önce hiç kimse frekansın enerji ile doğru orantılı olduğunu tahmin etmemişti (bu, biri ikiye katlandığında diğerinin de katlanacağı anlamına gelir). Doğal birimler olarak adlandırılan birimler altında, bir fotonun frekansını temsil eden sayı aynı zamanda enerjisini de temsil edecektir. O zaman denklem şöyle olur:
E = f
Yani enerji eşittir frekans.
Ancak fiziğin gelişiminde, enerjiyi ölçmek için kullanılan birimler ile zamanı (ve dolayısıyla frekansı) ölçmek için yaygın olarak kullanılan birimler arasında doğal bir bağlantı yoktu. Bu yüzden Planck'ın tüm sayıların doğru çıkmasını sağlamak için bulduğu formül şuydu:
E = h × f
ya da enerji, h çarpı frekansa eşittir. Bu h, keşfedenin adıyla Planck sabiti olarak adlandırılan bir sayıdır.
Kuantum mekaniği, belirli bir frekanstaki bir fotonun belirli bir miktarda enerjiye sahip bir foton anlamına geldiği bilgisine dayanır. Bu ilişkinin yanı sıra, belirli bir atom türü yalnızca belirli frekanslarda radyasyon yayabilir, bu nedenle de yalnızca belirli miktarlarda enerjiye sahip fotonlar yayabilir.
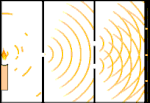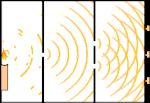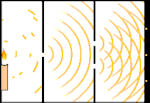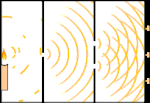
Çift yarık deneyi: ışık soldaki ışık kaynağından sağdaki saçaklara (siyah kenarla işaretlenmiş) gider.
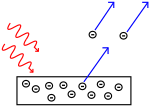
Fotoelektrik etki: fotonlar metale çarpar ve elektronlar uzağa itilir.
Tarih
Isaac Newton, ışığın bugün parçacık olarak adlandırdığımız çok küçük şeylerden oluştuğunu düşünüyordu (bunlara "Cisimcikler" diyordu). Christiaan Huygens ışığın dalgalardan oluştuğunu düşünüyordu. Bilim insanları bir şeyin aynı anda hem parçacık hem de dalga olamayacağını düşünüyordu.
Bilim insanları ışığın parçacıklardan mı yoksa dalgalardan mı oluştuğunu bulmak için deneyler yaptılar. Her iki fikrin de doğru olduğunu buldular - ışık bir şekilde hem dalgalar hem de parçacıklardan oluşuyordu. Thomas Young tarafından gerçekleştirilen Çift yarık deneyi, ışığın bir dalga gibi davranması gerektiğini gösterdi. Albert Einstein tarafından keşfedilen Fotoelektrik etki, ışığın belirli miktarlarda enerji taşıyan parçacıklar gibi davranması gerektiğini ve enerjilerin frekanslarıyla bağlantılı olduğunu kanıtladı. Bu deneysel sonuç kuantum mekaniğinde "dalga-parçacık ikiliği" olarak adlandırılır. Daha sonra fizikçiler, sadece ışığın değil, her şeyin hem dalga hem de parçacık gibi davrandığını keşfettiler. Ancak bu etki büyük cisimlerde çok daha küçüktür.
İşte kuantum mekaniğinin temel parçalarını keşfeden kişilerden bazıları: Max Planck, Albert Einstein, Satyendra Nath Bose, Niels Bohr, Louis de Broglie, Max Born, Paul Dirac, Werner Heisenberg, Wolfgang Pauli, Erwin Schrödinger, John von Neumann ve Richard Feynman. Çalışmalarını 20. yüzyılın ilk yarısında yapmışlardır.
Soldan sağa: Max Planck, Albert Einstein, Niels Bohr, Louis de Broglie, Max Born, Paul Dirac, Werner Heisenberg, Wolfgang Pauli, Erwin Schrödinger, Richard Feynman.
Planck'ın Ötesinde
Kuantum mekaniği formülleri ve fikirleri, parlayan hidrojenden gelen ışığı açıklamak için yapılmıştır. Atomun kuantum teorisi, diğer fikirlerin açıklayamadığı elektronun neden yörüngesinde kaldığını da açıklamak zorundaydı. Eski fikirlere göre elektron atomun merkezine düşmek zorundaydı çünkü başlangıçta kendi enerjisi tarafından yörüngede tutuluyordu, ancak yörüngesinde dönerken enerjisini hızla kaybediyordu. (Çünkü elektronların ve diğer yüklü parçacıkların ışık yaydıkları ve hız değiştirdiklerinde ya da döndüklerinde enerji kaybettikleri biliniyordu).
Hidrojen lambaları neon ışıkları gibi çalışır, ancak neon ışıklarının kendine özgü bir ışık rengi (ve frekansı) grubu vardır. Bilim insanları, tüm elementleri ürettikleri ışık renklerine göre tanımlayabileceklerini öğrendiler. Sadece frekansların nasıl belirlendiğini çözemediler.
Daha sonra Johann Balmer adında İsviçreli bir matematikçi, λ'nın (dalga uzunluğu için lambda) ne olacağını söyleyen bir denklem buldu:
λ = B ( n 2 n 2 - 4 ) n = 3 , 4 , 5 , 6 {\displaystyle \lambda =B\left({\frac {n^{2}}{n^{2}-4}}\right)\qquad \qquad n=3,4,5,6} 
Burada B, Balmer'in 364,56 nm'ye eşit olarak belirlediği bir sayıdır.
Bu denklem sadece bir hidrojen lambasından gelen görünür ışık için işe yarıyordu. Ancak daha sonra denklem daha genel hale getirildi:
1 λ = R ( 1 m 2 - 1 n 2 ) , {\displaystyle {\frac {1}{\lambda }}=R\left({\frac {1}{m^{2}}-{\frac {1}{n^{2}}}\right),} 
Burada R, 0,0110 nm'ye eşit olan Rydberg sabitidir−1 ve n, m'den büyük olmalıdır.
m ve n için farklı sayılar koyarak, birçok ışık türü (ultraviyole, görünür ve kızılötesi) için frekansları tahmin etmek kolaydır. Bunun nasıl çalıştığını görmek için Hyperphysics'e gidin ve sayfanın ortasından aşağıya inin. (Hidrojen için H = 1 kullanın.)
1908 yılında Walter Ritz, frekanslar arasındaki belirli boşlukların kendilerini nasıl tekrarladığını gösteren Ritz kombinasyon prensibini ortaya koymuştur. Bunun birkaç yıl sonra Werner Heisenberg için önemli olduğu ortaya çıktı.
1905 yılında Albert Einstein, Planck'ın fikrini kullanarak bir ışık demetinin foton adı verilen parçacıklardan oluştuğunu gösterdi. Her fotonun enerjisi frekansına bağlıdır. Einstein'ın fikri, kuantum mekaniğinde elektronlar, protonlar, nötronlar ve diğerleri gibi tüm atom altı parçacıkların aynı anda hem dalga hem de parçacık olduğu fikrinin başlangıcıdır. (Atomda elektronun dalga olarak bulunduğu atom resmine bakınız.) Bu, atom altı parçacıklar ve elektromanyetik dalgalar hakkında dalga-parçacık ikiliği adı verilen bir teoriye yol açmıştır. Bu, parçacıkların ve dalgaların ne biri ne de diğeri olduğu, ancak her ikisinin de belirli özelliklerine sahip olduğu yerdir.
1913 yılında Niels Bohr, elektronların bir atomun çekirdeği etrafında yalnızca belirli yörüngelerde yer alabileceği fikrini ortaya attı. Bohr'un teorisine göre, yukarıdaki denklemde m ve n olarak adlandırılan sayılar yörüngeleri temsil edebilir. Bohr'un teorisine göre elektronlar m yörüngesinde başlayıp n yörüngesinde sonlanabilir ya da bir elektron n yörüngesinde başlayıp m yörüngesinde sonlanabilir, dolayısıyla bir foton bir elektrona çarparsa enerjisi emilir ve elektron bu ekstra enerji nedeniyle daha yüksek bir yörüngeye hareket eder. Bohr'un teorisine göre, eğer bir elektron daha yüksek bir yörüngeden daha düşük bir yörüngeye düşerse, o zaman bir foton şeklinde enerji vermek zorunda kalacaktır. Fotonun enerjisi iki yörünge arasındaki enerji farkına eşit olacaktır ve bir fotonun enerjisi onun belirli bir frekansa ve renge sahip olmasını sağlar. Bohr'un teorisi atom altı olayların birçok yönüne iyi bir açıklama getirmiş, ancak parlayan hidrojen (ve parlayan neon veya başka herhangi bir element) tarafından üretilen ışık renklerinin her birinin neden kendine özgü bir parlaklığa sahip olduğunu ve parlaklık farklarının her element için her zaman aynı olduğunu yanıtlayamamıştır.
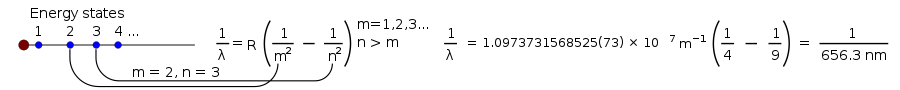
Niels Bohr teorisini ortaya attığında, bir hidrojen lambasının ürettiği ışıkla ilgili çoğu şey biliniyordu, ancak bilim adamları hala parlayan hidrojen tarafından üretilen çizgilerin her birinin parlaklığını açıklayamıyorlardı.
Werner Heisenberg her bir çizginin parlaklığını ya da "yoğunluğunu" açıklama işini üstlendi. Balmer'in bulduğu gibi basit bir kural kullanamadı. Her şeyi bir elektronun kütlesi (ağırlığı), bir elektronun yükü (statik elektrik gücü) ve diğer küçük miktarlar gibi şeyler açısından hesaplayan klasik fiziğin çok zor matematiğini kullanmak zorunda kaldı. Klasik fiziğin bir hidrojen lambasının ürettiği renk bantlarının parlaklığı için zaten cevapları vardı, ancak klasik teori dört ayrı renk bandı değil, sürekli bir gökkuşağı olması gerektiğini söylüyordu. Heisenberg'in açıklaması şöyledir:
Parlayan hidrojenin hangi frekanslarda ışık üreteceğini söyleyen bir yasa vardır. İlgili elektronlar atomun çekirdeğine (merkezine) yakın yörüngeler arasında hareket ederken aralıklı frekansları tahmin etmek zorundadır, ancak aynı zamanda elektronun daha uzak yörüngeler arasında hareket ederken ne yaptığına baktığımızda frekansların birbirine daha da yaklaşacağını tahmin etmek zorundadır. Ayrıca, dışarı çıktıkça frekanslar arasındaki yoğunluk farklarının birbirine daha da yaklaşacağını tahmin edecektir. Klasik fiziğin zaten tek bir denklem setiyle doğru cevapları verdiği yerde, yeni fizik aynı cevapları farklı denklemlerle vermek zorundadır.
Klasik fizik, fiziksel dünyanın matematiksel bir resmini yapmak için Fransız matematikçi Fourier'in yöntemlerini kullanır ve bu durumda, bazı ışıklardan gelen tüm frekanslardaki ışık yoğunluklarını veren tek bir düzgün eğri yapmak için bir araya gelen düzgün eğri koleksiyonlarını kullanır. Ancak bu doğru değildir çünkü bu düzgün eğri sadece yüksek frekanslarda ortaya çıkar. Daha düşük frekanslarda her zaman izole noktalar vardır ve hiçbir şey noktaları birbirine bağlamaz. Dolayısıyla, gerçek dünyanın bir haritasını çıkarmak için Heisenberg büyük bir değişiklik yapmak zorunda kaldı. Sadece doğada görülenlerle eşleşecek sayıları seçmek için bir şeyler yapması gerekiyordu. Bazen insanlar onun bu denklemleri "tahmin ettiğini" söyler, ancak o körü körüne tahminler yapmıyordu. İhtiyacı olanı buldu. Hesapladığı sayılar bir grafik üzerinde noktalar oluşturacaktı, ancak noktalar arasında bir çizgi olmayacaktı. Ve her hesaplama kümesi için sadece noktalardan oluşan bir "grafik" yapmak çok fazla kağıt israfına neden olur ve hiçbir şey yapılmasını sağlamazdı. Heisenberg, farklı frekanslar için yoğunlukları verimli bir şekilde tahmin etmenin ve bu bilgileri yararlı bir şekilde düzenlemenin bir yolunu buldu.
Balmer'in başlattığı ve Rydberg'in geliştirdiği yukarıda verilen deneysel kuralı kullanarak, Heisenberg'in istediği türden bir resim elde etmesine yardımcı olacak bir dizi sayının nasıl elde edileceğini görebiliriz:
Bu kurala göre elektron bir yörüngeden diğerine hareket ettiğinde, merkezden uzaklaşmasına ya da merkeze yaklaşmasına bağlı olarak enerji kazanır ya da kaybeder. Böylece bu yörüngeleri ya da enerji seviyelerini bir ızgaranın üst ve yan kısımlarına başlıklar halinde yerleştirebiliriz. Tarihsel nedenlerden dolayı en düşük yörüngeye n denir ve bir sonraki yörüngeye n - a denir, sonra n - b gelir ve bu böyle devam eder. Elektronlar aslında enerji kazanırken negatif sayılar kullanmaları kafa karıştırıcıdır, ancak bu böyledir.
Rydberg kuralı bize frekansları verdiğinden, elektronun nereye gittiğine bağlı olarak sayıları koymak için bu kuralı kullanabiliriz. Eğer elektron n'de başlayıp n'de bitiyorsa, o zaman gerçekten hiçbir yere gitmemiştir, yani enerji kazanmamış ve enerji kaybetmemiştir. Eğer elektron n-a'da başlayıp n'de bitiyorsa, o zaman daha yüksek bir yörüngeden daha düşük bir yörüngeye düşmüştür. Eğer bunu yaparsa enerji kaybeder ve kaybettiği enerji foton olarak ortaya çıkar. Fotonun belirli bir miktarda enerjisi vardır, e, ve bu e = h f denklemiyle belirli bir f frekansıyla ilişkilidir. Bu yüzden belirli bir yörünge değişikliğinin belirli bir ışık frekansı üreteceğini biliyoruz, f. Eğer elektron n'de başlar ve n - a'da biterse, bu daha düşük bir yörüngeden daha yüksek bir yörüngeye gittiği anlamına gelir. Bu sadece dışarıdan belirli bir frekansta ve enerjide bir foton geldiğinde, elektron tarafından emildiğinde ve ona enerjisini verdiğinde gerçekleşir ve elektronun daha yüksek bir yörüngeye çıkmasını sağlayan şey budur. Bu yüzden, her şeyi anlamlı kılmak için, bu frekansı negatif bir sayı olarak yazıyoruz. Belli bir frekansa sahip bir foton vardı ve şimdi o foton yok oldu.
Böylece şöyle bir tablo oluşturabiliriz; burada f(a←b), bir elektron b enerji durumundan (yörüngesinden) a enerji durumuna geçtiğinde oluşan frekansı ifade eder (Yine, diziler ters görünüyor, ancak orijinal olarak bu şekilde yazılmışlardır):
F ızgara
| Elektron Durumları | n | n-a | n-b | n-c | .... | |
| n | f(n←n) | f(n←n-a) | f(n←n-b) | f(n←n-c) | ..... | |
| n-a | f(n-a←n) | f(n-a←n-a) | f(n-a←n-b) | f(n-a←n-c) | ..... | |
| n-b | f(n-b←n) | f(n-b←n-a) | f(n-b←n-b) | f(n-b←n-c) | ..... | |
| geçiş.... | ..... | ..... | ..... | ..... |
Heisenberg ızgaraları bu şekilde yapmadı. Sadece aradığı yoğunlukları elde etmesini sağlayacak matematiği yaptı. Ancak bunu yapmak için iki genliği (bir dalganın ne kadar yüksek ölçtüğünü) çarparak yoğunluğu hesaplaması gerekiyordu. (Klasik fizikte yoğunluk, genliğin karesine eşittir.) Bu sorunu çözmek için garip görünümlü bir denklem oluşturdu, makalesinin geri kalanını yazdı, patronuna verdi ve tatile çıktı. Dr. Born onun komik denklemine baktı ve biraz çılgınca göründü. "Heisenberg bana bu garip şeyi neden verdi?" diye merak etmiş olmalı. Neden bu şekilde yapmak zorunda?" Sonra zaten çok iyi bildiği bir şeyin planına baktığını fark etti. Örneğin frekanslar için tüm matematiği yaparak yazabildiğimiz ızgara ya da tabloya matris demeye alışkındı. Heisenberg'in tuhaf denklemi de ikisini çarpmanın bir kuralıydı. Max Born çok ama çok iyi bir matematikçiydi. Çarpılan iki matris (ızgara) farklı şeyleri temsil ettiğinden (örneğin konum (x,y,z) ve momentum (mv) gibi), ilk matrisi ikinciyle çarptığınızda bir yanıt, ikinci matrisi ilk matrisle çarptığınızda başka bir yanıt elde edeceğinizi biliyordu. Matris matematiğini bilmemesine rağmen, Heisenberg bu "farklı cevaplar" problemini zaten görmüştü ve bu onu rahatsız etmişti. Ancak Dr. Born o kadar iyi bir matematikçiydi ki, ilk matris çarpımı ile ikinci matris çarpımı arasındaki farkın her zaman Planck sabiti h'nin negatif birin karekökü i ile çarpımını içereceğini gördü. Böylece Heisenberg'in keşfinden sonraki birkaç gün içinde, Heisenberg'in "belirsizlik ilkesi" olarak adlandırmaktan hoşlandığı şeyin temel matematiğine sahip oldular. Heisenberg "belirsiz" derken, elektron gibi bir şeyin sabitlenene kadar sabitlenemeyeceğini kastediyordu. Bu biraz da sürekli etrafta ezilen ve siz onu öldürmedikçe "tek bir yerde" kalamayan bir denizanasına benzer. Daha sonra insanlar bunu "Heisenberg'in belirsizlik ilkesi" olarak adlandırmayı alışkanlık haline getirdiler ve bu da birçok insanın elektronların ve benzeri şeylerin gerçekten "bir yerde" olduğunu ama bizim sadece kendi zihnimizde bu konuda belirsiz olduğumuzu düşünme hatasına düşmesine neden oldu. Bu düşünce yanlıştır. Heisenberg'in bahsettiği şey bu değildi. Bir şeyi ölçmekte zorlanmak bir sorundur, ancak Heisenberg'in bahsettiği sorun bu değildir.
Heisenberg'in fikrini kavramak çok zordur, ancak bir örnekle daha açık hale getirebiliriz. Öncelikle, bu ızgaraları "matris" olarak adlandırmaya başlayacağız, çünkü yakında matris çarpımı hakkında konuşmamız gerekecek.
Konum (q) ve momentum (p) olmak üzere iki tür ölçümle başladığımızı varsayalım. 1925 yılında Heisenberg buna benzer bir denklem yazdı:
Y ( n , n - b ) = ∑ a p ( n , n - a ) q ( n - a , n - b ) {\displaystyle Y(n,n-b)=\sum _{a}^{}\,p(n,n-a)q(n-a,n-b)}
(Eşlenik değişkenler momentum ve konum için denklem)
O bunu bilmiyordu, ama bu denklem iki matris (ızgara) yazmak ve bunları çarpmak için bir plan veriyor. Bir matrisi diğeriyle çarpmanın kuralları biraz karışıktır, ancak işte plana göre iki matris ve ardından bunların çarpımı:
P matrisi
| Elektron Durumları | n-a | n-b | n-c | .... | |
| n | p(n←n-a) | p(n←n-b) | p(n←n-c) | ..... | |
| n-a | p(n-a←n-a) | p(n-a←n-b) | p(n-a←n-c) | ..... | |
| n-b | p(n-b←n-a) | p(n-b←n-b) | p(n-b←n-c) | ..... | |
| geçiş.... | ..... | ..... | ..... | ..... |
q matrisi
| Elektron Durumları | n-b | n-c | n-d | .... | |
| n-a | q(n-a←n-b) | q(n-a←n-c) | q(n-a←n-d) | ..... | |
| n-b | q(n-b←n-b) | q(n-b←n-c) | q(n-b←n-d) | ..... | |
| n-c | q(n-c←n-b) | q(n-c←n-c) | q(n-c←n-d) | ..... | |
| geçiş.... | ..... | ..... | ..... | ..... |
Heisenberg'in 1925 tarihli makalesindeki ilgili denklemde belirtildiği gibi yukarıdaki iki matrisin çarpımı için matris şöyledir:
| Elektron Durumları | n-b | n-c | n-d | ..... |
| n | A | ..... | ..... | ..... |
| n-a | ..... | B | ..... | ..... |
| n-b | ..... | ..... | C | ..... |
Nerede?
A=p(n←n-a)*q(n-a←n-b)+p(n←n-b)*q(n-b←n-b)+p(n←n-c)*q(n-c←n-b)+.....
B=p(n-a←n-a)*q(n-a←n-c)+p(n-a←n-b)*q(n-b←n-c)+p(n-a←n-c)*q(n-c←n-c)+.....
C=p(n-b←n-a)*q(n-a←n-d)+p(n-b←n-b)*q(n-b←n-d)+p(n-b←n-c)*q(n-d←n-d)+.....
ve benzeri.
Matrisler ters çevrilirse, aşağıdaki değerler ortaya çıkacaktır:
A=q(n←n-a)*p(n-a←n-b)+q(n←n-b)*p(n-b←n-b)+q(n←n-c)*p(n-c←n-b)+.....
B=q(n-a←n-a)*p(n-a←n-c)+q(n-a←n-b)*p(n-b←n-c)+q(n-a←n-c)*p(n-c←n-c)+.....
C=q(n-b←n-a)*p(n-a←n-d)+q(n-b←n-b)*p(n-b←n-d)+q(n-b←n-c)*p(n-d←n-d)+.....
ve benzeri.
Çarpma işleminin sırasını değiştirmenin gerçekte çarpılan sayıları adım adım nasıl değiştirdiğine dikkat edin.
Parlayan hidrojen tarafından yayılan görünür ışık. (Nanometre cinsinden dalga boyları.)
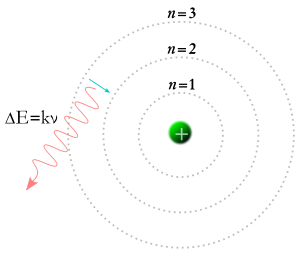
Bir elektron alt yörüngeye düşer ve bir foton oluşur.
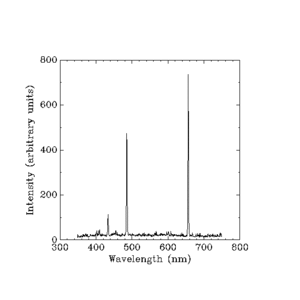
Rastgele birimlerde aralıklı yoğunluklar
Heisenberg'in Ötesinde
Werner Heisenberg'in çalışması bir tıkanıklığı açmış gibi görünüyordu. Çok geçmeden Louis de Broglie, Max Born, Paul Dirac, Wolfgang Pauli ve Erwin Schrödinger gibi kişilerden çok farklı açıklama biçimleri geldi. Bu fizikçilerin her birinin çalışmaları başlı başına bir öyküdür. Heisenberg ve daha önceki insanlar tarafından kullanılan matematiği anlamak çok zor değildir, ancak fizikçiler atomik dünyayı daha derinlemesine inceledikçe denklemler hızla çok karmaşık hale gelmiştir.
Diğer gizemler
Kuantum mekaniğinin ilk günlerinde Albert Einstein, eğer doğru olsaydı, kuantum mekaniğinin "uzakta ürkütücü eylem" olacağı anlamına geleceğini öne sürdü. Kuantum mekaniğinin doğru olduğu ve Einstein'ın kuantum mekaniğini reddetmek için bir neden olarak kullandığı şeyin gerçekten gerçekleştiği ortaya çıktı. Belirli kuantum olayları arasındaki bu tür "ürkütücü bağlantı" artık "kuantum dolanıklığı" olarak adlandırılmaktadır.
Bir deney iki şeyi (fotonlar, elektronlar, vs.) bir araya getirdiğinde, bunların kuantum mekaniğinde ortak bir tanımı paylaşmaları gerekir. Daha sonra ayrıldıklarında, aynı kuantum mekaniksel tanımlamayı veya "durumu" korurlar. Diyagramda, bir özellik (örneğin, "yukarı" spin) kırmızı ile çizilmiş ve eşi (örneğin, "aşağı" spin) mavi ile çizilmiştir. Mor bant, örneğin iki elektron bir araya getirildiğinde çiftin her iki özelliği de paylaştığı anlamına gelir. Yani her iki elektron da ya yukarı spin ya da aşağı spin gösterebilir. Daha sonra ayrıldıklarında, biri Dünya'da kaldığında ve diğeri Alpha Centauri yıldızının bir gezegenine gittiğinde, her ikisi de hala her iki spine de sahiptir. Başka bir deyişle, her biri kendisini yukarı spinli ya da aşağı spinli bir elektron olarak göstermeye "karar verebilir". Ancak daha sonra birisi diğerini ölçerse, o da kendisini ters spinli olarak göstermeye "karar vermelidir".
Einstein, bu kadar büyük bir mesafede bir elektronu spinini göstermeye zorlamanın, diğer elektronun bir şekilde zıt bir özellik göstermesini sağlayacağını düşünmenin çılgınlık olduğunu savundu. İki elektronun başından beri spinli ya da spinsiz olması gerektiğini, ancak kuantum mekaniğinin her bir elektronun hangi özelliğe sahip olduğunu öngöremeyeceğini söyledi. Tahmin edememek, sadece birine doğru deneyle bakabilmek, kuantum mekaniğinin önemli bir şeyi açıklayamadığı anlamına geliyordu. Bu nedenle Einstein, kuantum mekaniğinde büyük bir delik olduğunu söyledi. Kuantum mekaniği eksikti.
Daha sonra, deneylerin yanılanın Einstein olduğunu gösterdiği ortaya çıktı.
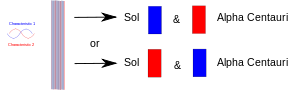
İki dolaşık parçacık ayrılır: biri Dünya'da diğeri uzak bir gezegene götürülür. Bunlardan birini ölçmek onu hangi rolü alacağına "karar vermeye" zorlar ve diğeri de (bundan sonra) her ölçüldüğünde diğer rolü almak zorundadır.
Heisenberg belirsizlik ilkesi
1925 yılında Werner Heisenberg, bir parçacığın nerede olduğu hakkında ne kadar çok şey bilirsek, ne kadar hızlı ve hangi yönde gittiği hakkında o kadar az şey bilebileceğimizi söyleyen Belirsizlik ilkesini tanımladı. Başka bir deyişle, küçük bir şeyin hızı ve yönü hakkında ne kadar çok şey bilirsek, konumu hakkında o kadar az şey bilebiliriz. Fizikçiler bu tür tartışmalarda genellikle hızdan bahsetmek yerine momentumdan bahsederler. Momentum, bir şeyin belirli bir yöndeki hızının kütlesiyle çarpımıdır.
Heisenberg'in belirsizlik ilkesinin ardındaki neden, bir parçacığın hem konumunu hem de momentumunu asla bilemeyeceğimizi söyler. Işık bol miktarda bulunan bir parçacık olduğu için diğer parçacıkların ölçümünde kullanılır. Bunu ölçmenin tek yolu, ışık dalgasını parçacıktan sektirmek ve sonuçları kaydetmektir. Eğer yüksek enerjili ya da yüksek frekanslı bir ışık demeti kullanılırsa, tam olarak nerede olduğunu söyleyebiliriz, ancak ne kadar hızlı gittiğini söyleyemeyiz. Bunun nedeni, yüksek enerjili fotonun parçacığa enerji aktarması ve parçacığın hızını değiştirmesidir. Düşük enerjili bir foton kullanırsak, ne kadar hızlı gittiğini söyleyebiliriz, ancak nerede olduğunu söyleyemeyiz. Bunun nedeni daha uzun dalga boyuna sahip ışık kullanıyor olmamızdır. Daha uzun dalga boyu, parçacığın dalga boyunca herhangi bir yerde olabileceği anlamına gelir.
İlke aynı zamanda, ne kadar uğraşırsak uğraşalım, herhangi bir parçacık (çok küçük bir şey) hakkında her ikisini de bilemeyeceğimiz birçok ölçüm çifti olduğunu söyler. Böyle bir çiftten biri hakkında ne kadar çok şey öğrenirsek, diğeri hakkında o kadar az şey bilebiliriz.
Albert Einstein bile böylesine tuhaf bir kavramı kabul etmekte zorlanmış ve ünlü bir tartışmada "Tanrı zar atmaz" demiştir. Buna Danimarkalı fizikçi Niels Bohr'un yanıtı meşhurdur: "Einstein, Tanrı'ya ne yapacağını söyleme".
QM'in Kullanım Alanları
Elektronlar her atomun çekirdeğini çevreler. Kimyasal bağlar atomları birbirine bağlayarak molekülleri oluşturur. Bir kimyasal bağ, elektronlar bu atomlar arasında paylaşıldığında iki atomu birbirine bağlar. Dolayısıyla QM, kimyasal bağın ve kimyanın fiziğidir. QM, moleküllerin nasıl oluştuğunu ve özelliklerinin ne olduğunu anlamamıza yardımcı olur.
QM, yıldızlar ve hatta tüm evren gibi büyük şeyleri anlamamıza da yardımcı olabilir. QM, Büyük Patlama olarak adlandırılan evrenin nasıl başladığına dair teorinin çok önemli bir parçasıdır.
Maddeden yapılmış her şey, yerçekimi adı verilen temel bir kuvvet nedeniyle diğer maddelere doğru çekilir. Einstein'ın yerçekimini açıklayan teorisine genel görelilik teorisi denir. Modern fizikteki bir sorun, QM'in bazı sonuçlarının genel görelilik teorisiyle uyuşmuyor gibi görünmesidir.
QM, fiziğin tüm elektronik teknolojisinin neden olduğu gibi çalıştığını açıklayabilen kısmıdır. Dolayısıyla QM bilgisayarların nasıl çalıştığını açıklar, çünkü bilgisayarlar elektronik makinelerdir. Ancak 1950 ya da 1960'lardaki ilk bilgisayar donanımlarının tasarımcılarının QM hakkında düşünmelerine gerek yoktu. O dönemde radyo ve televizyon tasarımcıları da QM hakkında düşünmemişlerdir. Ancak, son yılların daha güçlü entegre devrelerinin ve bilgisayar bellek teknolojilerinin tasarımı QM'yi gerektirmektedir.
QM ayrıca aşağıdaki gibi teknolojileri de mümkün kılmıştır:
QM'i öğrenmek neden zordur?
QM çeşitli nedenlerden dolayı zorlu bir konudur:
- QM, olayları çocukken dünya hakkında öğrendiklerimizden çok farklı şekillerde açıklar.
- QM'yi anlamak cebir ve basit hesaptan daha fazla matematik gerektirir. Ayrıca matris cebiri, karmaşık sayılar, olasılık teorisi ve kısmi diferansiyel denklemler de gerektirir.
- Fizikçiler QM'nin bazı denklemlerinin bize gerçek dünya hakkında ne söylediğinden emin değiller.
- QM, atomların ve atom altı parçacıkların günlük hayatımızda gördüğümüz hiçbir şeye benzemeyen garip şekillerde davrandığını öne sürer.
- QM son derece küçük olan şeyleri tanımlar, bu nedenle bazılarını özel ekipman olmadan göremeyiz ve birçoğunu hiç göremeyiz.
QM, doğayı genellikle bilim hakkında düşündüğümüzden farklı bir şekilde tanımlar. Bize bazı şeylerin kesinlikle gerçekleşeceğini söylemek yerine, gerçekleşme olasılığının ne kadar olduğunu söyler.
Buna bir örnek Young'ın çift yarık deneyidir. Bir lazerden bir fotoğraf filmine tek fotonlar (tek ışık birimleri) atarsak, banyo edilmiş film üzerinde tek bir ışık noktası görürüz. Araya bir metal levha koyar ve levhada çok dar iki yarık açarsak, metal levhaya çok sayıda foton ateşlediğimizde ve bunlar yarıklardan geçmek zorunda kaldıklarında, o zaman dikkate değer bir şey görürüz. Banyo edilmiş film tabakası boyunca bir dizi parlak ve karanlık bant göreceğiz. Parlak bantların tam olarak nerede olacağını ve onları oluşturan ışığın ne kadar parlak olduğunu söylemek için matematiği kullanabiliriz, yani her bir banda kaç foton düşeceğini önceden söyleyebiliriz. Ancak süreci yavaşlatır ve her bir fotonun ekranda nereye düştüğünü görürsek, bir sonraki fotonun nerede görüneceğini asla önceden söyleyemeyiz. Bir fotonun merkezdeki parlak banda düşme olasılığının yüksek olduğunu ve merkezden gittikçe uzaklaşan bantlarda bir fotonun görünme olasılığının gittikçe azaldığını kesin olarak bilebiliriz. Yani bantların merkezde en parlak olacağını ve uzaklaştıkça daha da sönükleşeceğini kesin olarak biliyoruz. Ancak hangi fotonun hangi banda gireceğini asla kesin olarak bilemeyiz.
QM teorisinin garip sonuçlarından biri de "Schrödinger'in kedisi" etkisidir. Bir parçacığın konumu, hareket hızı, hareket yönü ve "spin" gibi belirli özellikleri, bir şey onları ölçene kadar konuşulamaz (örneğin, bir elektrondan seken bir foton, onun konumunun ölçümü olarak sayılır). Ölçümden önce parçacık, özelliklerinin aynı anda birçok değere sahip olduğu bir "durumların süperpozisyonu" içindedir. Schrödinger, kuantum mekaniğinin, eğer bir şey (bir kedinin yaşamı ya da ölümü gibi) bir kuantum olayı tarafından belirleniyorsa, o zaman durumunun kuantum olayından kaynaklanan durum tarafından belirleneceğini söylüyor gibi göründüğünü söyledi, ancak sadece birisinin kuantum olayının durumuna baktığı zaman. Kuantum olayının durumuna bakılmadan önceki zamanda, belki de "yaşayan ve ölü kedi (ifadeyi mazur görün) [birbirine] karışmış veya eşit parçalara ayrılmıştır."
İndirgenmiş Planck sabiti
İnsanlar genellikle ℏ {\displaystyle \hbar } sembolünü kullanır. 
"h-bar" olarak adlandırılır. ℏ = h 2 π {\displaystyle \hbar ={\frac {h}{2\pi }}}
. H-bar bir açısal momentum birimidir. Bu yeni birim atomlardaki elektronların yörüngelerini tanımlamak için kullanıldığında, yörüngedeki herhangi bir elektronun açısal momentumu her zaman bir tam sayıdır.
Örnek
Bir boyutlu bir kuyudaki parçacık, bir parçacığın enerjisinin yalnızca belirli değerlere sahip olabileceğini gösteren en basit örnektir. Enerjinin "kuantize" olduğu söylenir. Kuyu, bir aralık içinde sıfır potansiyel enerjiye sahiptir ve bu aralığın dışındaki her yerde sonsuz potansiyel enerjiye sahiptir. x {\displaystyle x}
yönünde 1-boyutlu durum için, zamandan bağımsız Schrödinger denklemi şu şekilde yazılabilir:
- ℏ 2 2 m d 2 ψ d x 2 = E ψ . {\displaystyle -{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}\psi }{dx^{2}}}=E\psi . } 
Diferansiyel denklemleri kullanarak, ψ {\displaystyle \psi }
olması gerektiğini görebiliriz.
ψ = A e i k x + B e - i k x E = ℏ 2 k 2 2 m {\displaystyle \psi =Ae^{ikx}+Be^{-ikx}\;\;\;\;\;E={\frac {\hbar ^{2}k^{2}}{2m}}} 
veya
ψ = C sin k x + D cos k x {\displaystyle \psi =C\sin kx+D\cos kx\; }
(Euler formülü ile)
Kutunun duvarları, dalga fonksiyonunun özel bir biçime sahip olması gerektiği anlamına gelir. Duvarlar sonsuz uzunlukta olduğunda parçacığın dalga fonksiyonu sıfır olmalıdır. Her duvarda:
ψ = 0 a t x = 0 , x = L {\displaystyle \psi =0\;\mathrm {at} \;\;x=0,\;x=L} 
x = 0 olduğunu düşünün
- sin 0 = 0, cos 0 = 1. ψ = 0'ı sağlamak için {\displaystyle \scriptstyle \psi =0\; }
cos terimi kaldırılmalıdır. Dolayısıyla D = 0
Şimdi düşünün: ψ = C sin k x {\displaystyle \scriptstyle \psi =C\sin kx\; } 
- x = L'de, ψ = C sin k L = 0 {\displaystyle \scriptstyle \psi =C\sin kL=0\; }
- C = 0 ise ψ = 0 {\displaystyle \scriptstyle \psi =0\; } tüm x için. Bu çözüm kullanışlı değildir.
- bu nedenle sin kL = 0 doğru olmalıdır, bu da bize
k L = n π n = 1 , 2 , 3 , 4 , 5 , . . . {\displaystyle kL=n\pi \;\;\;n=1,2,3,4,5,...\; } 
n {\displaystyle n}
bir tamsayı olması gerektiğini görebiliriz. Bu, parçacığın yalnızca özel enerji değerlerine sahip olabileceği ve aradaki enerji değerlerine sahip olamayacağı anlamına gelir. Bu, enerji "kuantizasyonuna" bir örnektir.
İlgili sayfalar
- Elektromanyetik dalga
- Elektron
- Foton
- Kuantum dolanıklığı
- Schrödinger denklemi
Sorular ve Yanıtlar
S: Kuantum mekaniği nedir?
C: Kuantum mekaniği, evrenin atomlardan daha küçük bir ölçekte nasıl çalıştığını açıklayan bir fizik dalıdır. Kuantum fiziği veya kuantum teorisi olarak da bilinir.
S: "Kuantum" terimi ne anlama gelir?
C: "Kuantum" terimi Latince'den gelir ve "ne kadar" anlamına gelir. Bir enerji kuantumu mümkün olan en az miktardır (veya en az ekstra miktardır) ve kuantum mekaniği bu enerjinin nasıl hareket ettiğini veya etkileştiğini açıklar.
S: Atom altı parçacıklar nedir?
C: Atom altı parçacıklar, protonlar, nötronlar ve elektronlar gibi atomları oluşturan parçacıklardır. Atomlardan bile daha küçüktürler.
S: Kuantum mekaniği bu parçacıkların nasıl çalıştığını nasıl açıklar?
C: Kuantum mekaniği, davranışlarını ve birbirleriyle etkileşimlerini anlamak amacıyla atom altı parçacıkları ve elektromanyetik dalgaları incelemek için matematiksel kurallar sağlar.
S: Dalga-parçacık ikiliği nedir?
C: Dalga-parçacık ikiliği, hem parçacıkların hem de dalgaların birbirleri gibi davranabileceği gerçeğini ifade eder - bunlar iki ayrı varlık değil, daha ziyade her ikisinin tek bir fenomende birleşmesi gibi bir şeydir.
S: Kuantum mekaniği kullanılarak modern fizik nasıl tanımlanabilir?
C: Modern fizik ve kimya, kuantum mekaniğinin matematiksel kuralları uygulanarak açıklanabilir.
