Eşlenik değişkenler, kendileriyle

Eşlenik değişkenler, kendileriyle belirli bir matematiksel işlem yaptığınızda aynı sonucu vermeyen özel değişken çiftleridir (x, y, z gibi). Bu, x*y'nin y*x'e eşit olmadığı anlamına gelir. Burada * çarpma anlamına gelmez. Toplama, çıkarma, bölme veya bu durumda mantıklı olan herhangi bir işlem anlamına gelebilir.

Bir fizikçi olan Werner Heisenberg ve çalışma arkadaşları, kuantum fiziğindeki olayları tanımlamak ve tahmin etmek için klasik fizikte çalışılan denklemleri kullandılar. Momentum (kütle çarpı hız, P ile gösterilir) ve konumun (Q ile gösterilir) eşlenik değişkenler olduğunu keşfetti. Bu, kuantum fiziğinde P*Q'nun Q*P'ye eşit olmadığı anlamına gelir.

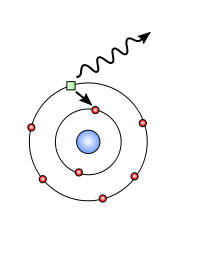
İşte hidrojen atomundaki bir elektronun (küçük yeşil şey) enerjisini hesaplamak için iki özel denklem.

Electron falls from higher to lower orbit and emits a photon

İlk denklem momentum ve konumun çarpımını bulmak için kullanılabilir:

Y ( n , n - b ) = ∑ a p ( n , n - a ) q ( n - a , n - b ) {\displaystyle Y(n,n-b)=\sum _{a}^{}\,p(n,n-a)q(n-a,n-b)} $Y(n,n-b)=\sum _{{a}}^{{}}\,p(n,n-a)q(n-a,n-b)$

İkinci denklem konum ve momentum çarpımını hesaplamak için kullanılabilir:

Z ( n , n - b ) = ∑ a q ( n , n - a ) p ( n - a , n - b ) {\displaystyle Z(n,n-b)=\sum _{a}^{}\,q(n,n-a)p(n-a,n-b)} $Z(n,n-b)=\sum _{a}^{}\,q(n,n-a)p(n-a,n-b)$

Bir süre sonra, başka bir fizikçi olan Max Born, P*Q, Q*P'ye eşit olmadığı için Q*P eksi P*Q sonucunun sıfır olmadığını keşfetti. ("Eksi", "3 - 2" ile aynı eksi değildir. Aynı adı taşıyan farklı bir şeydir).

Born bunu öğrendi:

Q ∗ P - P ∗ Q = i h 2 π {\displaystyle {Q*P-P*Q={\frac {ih}{2\pi }}}} ${Q*P-P*Q={\frac {ih}{2\pi }}}$

[Q sembolü konum matrisi, P momentum matrisi, i karmaşık bir sayı ve h Planck sabitidir, kuantum mekaniğinde çokça karşımıza çıkan bir sayıdır].

Eşlenik değişkenlerin Fizikte, Kimyada ve bilimin diğer birçok alanında uygulamaları vardır.

Bazı ilgili konular

Heisenberg'in belirsizlik ilkesi

Sorular ve Yanıtlar

S: Eşlenik değişkenler nedir?

C: Eşlenik değişkenler, kendileriyle belirli bir matematiksel işlem yaptığınızda aynı sonucu vermeyen özel değişken çiftleridir (x, y, z gibi). Bu, x*y'nin y*x'e eşit olmadığı anlamına gelir.

S: Eşlenik değişkenleri kim keşfetti?

C: Fizikçi Werner Heisenberg ve çalışma arkadaşları, kuantum fiziğindeki olayları tanımlamak ve tahmin etmek için klasik fizikte çalışılan denklemleri kullandılar. Momentum (kütle çarpı hız, P ile gösterilir) ve konumun (Q ile gösterilir) eşlenik değişkenler olduğunu keşfetti.

S: Momentum ve konumun çarpımını hesaplamak için hangi denklem kullanılabilir?

C: Momentum ve konumun çarpımını bulmak için ilk denklem kullanılabilir: Y(n,n-b)=∑a p(n,n-a)q(n-a,n-b).

S: Konum ve momentumun çarpımını hesaplamak için hangi denklem kullanılabilir?

C: Konum ve momentumun çarpımını hesaplamak için ikinci denklem kullanılabilir: Z(n,n-b)=∑a q(n,n-a)p(n-a, n-b).

S: Max Born eşlenik değişkenler hakkında ne keşfetti?

C: Max Born, P*Q, Q*P'ye eşit olmadığı için Q*P eksi P*Q sonucunun sıfır olmadığını keşfetti. Ayrıca Q-P - P-Q = ih/2π olduğunu da buldu.

S: Planck sabiti kuantum mekaniğinde nasıl ortaya çıkıyor?

C: Planck sabiti kuantum mekaniğinde Max Born'un eşlenik değişken çarpımlarını hesaplamak için kullandığı denklemde, özellikle de eşittir işaretinin bir tarafında h/2π olarak ortaya çıkar.

S: Eşlenik değişkenlerin hangi alanlarda uygulamaları vardır?

C: Eşlenik değişkenlerin Fizik, Kimya ve diğer bilim alanlarının her yerinde uygulamaları vardır.