Heisenberg'in belirsizlik ilkesi

Gözlemci etkisi ile karışıklık

Tarihsel olarak belirsizlik ilkesi, fizikte gözlemci etkisi olarak adlandırılan benzer bir etkiyle karıştırılmıştır. Bu, bazı sistemlerin ölçümlerinin sistemleri etkilemeden yapılamayacağını söyler. Heisenberg, kuantum belirsizliğinin fiziksel bir "açıklaması" olarak kuantum düzeyinde böyle bir gözlemci etkisi önermiştir.

Ancak, belirsizlik ilkesinin tüm dalga benzeri sistemlerin bir özelliği olduğu artık açıktır. Kuantum mekaniğinde basitçe tüm kuantum nesnelerinin madde dalgası doğası nedeniyle ortaya çıkar. Dolayısıyla, belirsizlik ilkesi aslında kuantum sistemlerinin temel bir özelliğini ifade eder ve mevcut teknolojinin gözlemsel başarısı hakkında bir ifade değildir. "Ölçüm" sadece bir fizikçi-gözlemcinin yer aldığı bir süreç değil, herhangi bir gözlemciden bağımsız olarak klasik ve kuantum nesneler arasındaki herhangi bir etkileşim anlamına gelir.

Belirsizlik fikri

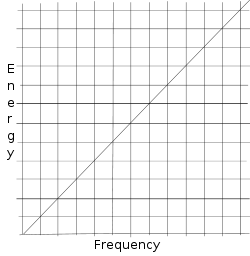
Belirsizlik ilkesi Werner Heisenberg'in matris mekaniğinden gelmektedir. Max Planck, bir ışık biriminin enerjisinin o ışık biriminin frekansıyla orantılı olduğunu ( E ∝ ν {\displaystyle E\propto \nu } ) ve enerji miktarının bir orantı sabiti kullanılarak joule gibi bilinen terimlerle ifade edilebileceğini zaten biliyordu. Dünyaya kazandırdığı bu sabit şimdi Planck sabiti olarak adlandırılıyor ve h harfiyle temsil ediliyor. Kuantum mekaniğini ifade etmek için matrisler kullanıldığında, fizikçinin bulmaya çalıştığı cevabı veren üçüncü bir matris elde etmek için genellikle iki matrisin çarpılması gerekir. Ancak P (momentum için) gibi bir matrisi X (konum için) gibi bir matrisle çarpmak, X'i P ile çarptığınızda elde ettiğinizden farklı bir cevap matrisi verir. P'yi X ve X'i P ile çarpmanın ve ardından bunları karşılaştırmanın sonucu her zaman bir faktör olarak Planck sabitini içerir. Planck sabitini yazmak için kullanılan sayı her zaman kullanılan ölçüm sistemine bağlı olacaktır. (Belirli bir ölçüm sisteminde sayısal değeri birdir.) Sağdaki diyagramda frekansın enerjiye oranını gösteren çizginin eğimi de seçilen ölçüm sistemine bağlı olacaktır.

Aşağıdaki diyagramlar hem konumu hem de momentumu ölçmeye çalıştığımızda neler olduğunu göstermektedir.

Bu matematiksel keşfin pratik sonucu, bir fizikçi konumu daha açık hale getirdiğinde momentumun daha az açık hale gelmesi ve fizikçi momentumu daha açık hale getirdiğinde konumun daha az açık hale gelmesidir. Heisenberg şeylerin "belirsiz" olduğunu söylerken, diğer insanlar "belirsiz" olduklarını söylemeyi severdi. Ancak matematik, belirsiz ya da "bulanık" olanın dünyadaki şeyler olduğunu, sadece insanların neler olup bittiğinden emin olmadığını göstermektedir.

Geniş delik, keskin odak


Boşluğu daraltmak fotonun ortada nerede olduğunun kesinliğini artırır, ancak daha sonra oradan sağdaki algılama ekranına olan yönü de buna bağlı olarak daha belirsiz hale gelir.


Dar delik, dağınık odak


Ortadaki boşluğun yaylarla askıya alınması momentumun ölçülmesini sağlar, ancak boşluğu öngörülemeyen bir şekilde hareket ettirir, böylece fotonun ortadaki konumu hakkındaki bilgi kaybolur.


Yaya monteli delik momentum ölçer

Belirsizliği matematiksel forma sokmak

Burada, daha sonra Heisenberg'in belirsizlik ilkesinde gösterilecek olan temel fikri veren ilk denklemi göstereceğiz.

Heisenberg'in 1925 tarihli çığır açan makalesinde matrisler kullanılmaz ve hatta matrislerden bahsedilmez. Heisenberg'in büyük başarısı, hidrojen radyasyonunun "ilgili fiziksel niteliklerini (geçiş frekansları ve genlikleri) ilke olarak benzersiz bir şekilde belirleyebilen şema" idi.

Heisenberg çığır açan makalesini yazdıktan sonra, düzeltmesi için öğretmenlerinden birine verdi ve tatile çıktı. Max Born, Heisenberg'in bile bir sorun olduğunu düşündüğü denklemler ve bağlaşımsız denklemler karşısında şaşkına döndü. Birkaç gün sonra Born, bu denklemlerin matrisleri yazmak için yönergeler olduğunu fark etti. Matrisler o zamanın matematikçileri için bile yeni ve garipti, ancak onlarla nasıl matematik yapılacağı zaten açıkça biliniyordu. Heisenberg izinden dönmeden önce o ve birkaç kişi daha her şeyi matris formunda çözdü ve birkaç ay içinde matris formundaki yeni kuantum mekaniği onlara başka bir makalenin temelini verdi.

Max Born, pq ve qp'yi temsil eden matrisler hesaplandığında bunların eşit olmayacağını gördü. Heisenberg de aynı şeyi kendi özgün yazım biçimi açısından zaten görmüştü ve Heisenberg, Born için neredeyse apaçık olan şeyi, yani pq ve qp cevap matrisleri arasındaki farkın her zaman Heisenberg'in özgün matematiğinden çıkan iki faktörü içereceğini tahmin etmiş olabilir: Planck sabiti h ve negatif birin karekökü olan i. Yani Heisenberg'in "belirsizlik ilkesi" (genellikle belirsizlik ilkesi olarak bilinir) olarak adlandırmayı tercih ettiği fikrin ta kendisi Heisenberg'in orijinal denklemlerinde saklıydı.

Heisenberg, bir elektron enerji seviyesini değiştirdiğinde ve böylece atomunun merkezine yaklaştığında veya merkezinden uzaklaştığında atomda meydana gelen değişikliklere ve özellikle de bir elektronun iki adımda daha düşük bir enerji durumuna düştüğü durumlara bakıyordu. Max Born, Heisenberg'in bir atomda n enerji seviyesinden n-b enerji seviyesine olan bir değişimin çarpımı olan C'yi bulmak için kullandığı ve atomdaki bir elektronun n enerji durumu ile n-a enerji durumu arasındaki enerji değişiminin ürettiği A adlı bir şeydeki (örneğin bir fotonun frekansı olabilir) bir değişimin B adlı bir şeydeki (örneğin bir değişimin genliği olabilir) başka bir enerji durumundaki n-a'dan n-b'ye olan değişimin ürettiği bir sonraki değişimle çarpımının toplamını almayı içeren garip "tarifini" nasıl aldığını açıkladı:)

C ( n , n - b ) = ∑ a A ( n , n - a ) B ( n - a , n - b ) {\displaystyle C(n,n-b)=\sum _{a}^{}\,A(n,n-a)B(n-a,n-b)}

ve çığır açan bir şey keşfettim:

Heisenberg.... ...örnekler üzerinde düşünerek.... bu kuralı buldu. Bu 1925 yazında oldu. Heisenberg...izin aldı...ve makalesini yayınlamam için bana teslim etti....

Heisenberg'in çarpma kuralı beni rahat bırakmadı ve bir haftalık yoğun düşünce ve denemeden sonra aniden cebirsel bir teoriyi hatırladım....Bu tür ikinci dereceden diziler matematikçiler için oldukça tanıdıktır ve belirli bir çarpma kuralıyla birlikte matrisler olarak adlandırılır. Bu kuralı Heisenberg'in kuantum koşuluna uyguladım ve diyagonal elemanlar için geçerli olduğunu gördüm. Geriye kalan elemanların ne olması gerektiğini tahmin etmek kolaydı, yani boş; ve hemen önümde garip formül duruyordu

Q P - P Q = i h 2 π {\displaystyle {QP-PQ={\frac {ih}{2\pi }}}}
[Q
 sembolü yer değiştirme matrisi, P momentum matrisi, i negatif birin karekökü ve h Planck sabitidir].

Daha sonra Heisenberg keşfini başka bir matematiksel forma soktu:

Δ x Δ p ≥ ℏ 2 {\displaystyle \Delta x\,\Delta p\geq {\frac {\hbar }{2}}}

(Özel sembol ℏ {\displaystyle {\hbar }} "h-bar" veya 'indirgenmiş Planks sabiti' olarak adlandırılır ve h 2 π {\displaystyle {\frac {h}{2\pi }} 'ye eşittir).

Matematik, gerçek dünyada olan şeyleri tanımlamanın bir yoludur. Bir şeyin hem tam konumunu hem de tam kütlesini, yolunu ve hızını aynı anda elde etmenin kolay olacağını düşünebilirsiniz. Ancak, gerçekte cevabınızı almak için iki şey yapmanız gerekir. Eğer bir yerde büyük bir dağın uçurumuna saplanmış bir merminin konumunu ve momentumunu ölçüyorsanız, bu basit bir meseledir. Dağ hiçbir yere gitmiyor gibi görünür, mermi de öyle. Dolayısıyla konumu bilinmektedir ve hızı 0'dır, dolayısıyla momentumu da 0'dır. Ancak mermi bir silah ile hedef arasında bir yerdeyse, herhangi bir andaki konumunu elde etmek zor olacaktır. Yapabileceğimiz en iyi şey, çok hızlı deklanşörü olan bir kamera kullanarak fotoğrafını çekmek olabilir. Ancak deklanşöre tek bir kez basmak size tek bir şey verecektir, merminin t zamanındaki konumu. Momentumu elde etmek için merminin yoluna bir parafin bloğu koyabilir ve mermiyi durdurduğunda parafin bloğunun nasıl hareket ettiğini ölçebiliriz. Ya da, eğer merminin kütlesini biliyorsak, iki resimden oluşan bir dizi çekebilir, merminin iki konumu arasındaki farkı ve iki görünüşü arasındaki zamanı bilerek hızı hesaplayabiliriz. Bunu nasıl yaparsak yapalım, kütleyi, konumu ve görünümler arasındaki zamanı ölçmemiz gerekir. Bu durumda hangi ölçümü önce, hangisini sonra yapacağımızı seçmemiz gerekir. Ölçümlerimizin hangi sırada yapıldığının bir önemi yok gibi görünüyor. Merminin kütlesini ölçtükten sonra konumunu iki kez ölçmek ya da merminin konumunu iki kez ölçtükten sonra mermiyi geri getirip kütlesini ölçmek bir fark yaratmaz, değil mi? Sonuçta, mermiyi tarttığımızda ya da fotoğrafını çektiğimizde mermiye hiçbir şey yapmamış oluruz.

Ancak elektron gibi bir şeyi ölçtüğümüz çok küçük ölçekte, her ölçüm ona bir şey yapar. Eğer önce konumu ölçersek, bu süreçte onun momentumunu değiştiririz. Eğer önce elektronun momentumunu ölçersek, bu süreçte elektronun konumunu değiştirmiş oluruz. Umudumuz bunlardan birini ölçmek ve sonra hiçbir şey değişmeden diğerini ölçmek olurdu, ancak ölçümümüzün kendisi bir değişiklik yapar ve yapabileceğimiz en iyi şey, elektronu ölçerek ona katkıda bulunduğumuz enerjiyi en aza indirmektir. Bu minimum enerji miktarı, faktörlerinden biri olarak Planck sabitine sahiptir.

Belirsizlik matris matematiğinin ötesine geçer

Heisenberg'in belirsizlik ilkesi, "yeni" kuantum fiziğinin ilk denklemlerinde bulundu ve teori matris matematiği kullanılarak verildi. Bununla birlikte, belirsizlik ilkesi doğayla ilgili bir gerçektir ve Erwin Schrödinger tarafından yapılan denklemler gibi kuantum fiziği hakkında konuşmanın diğer yollarında da ortaya çıkar.

Doğadaki belirsizlik, insanların belirsizliği değil

Heisenberg'in keşfettiği şeye bakmanın çok farklı iki yolu olmuştur: Bazı insanlar doğada olan şeylerin "belirli" olduğunu, yani her şeyin belirli bir kurala göre gerçekleştiğini ve bilmemiz gereken her şeyi bilebilseydik bir sonraki adımda ne olacağını her zaman söyleyebileceğimizi düşünüyor. Diğer insanlar ise doğada olan şeylerin sadece olasılık tarafından yönlendirildiğini ve sadece ortalama olarak nasıl davranacaklarını bilebileceğimizi düşünürler - ama biz bunu çok kesin olarak biliyoruz.

Fizikçi John Stewart Bell, ilk yolun doğru olamayacağını kanıtlamanın bir yolunu keşfetti. Çalışması Bell teoremi veya Bell Eşitsizliği olarak adlandırılır.

Popüler kültür

"Kuantum sıçraması" ya da "kuantum sıçraması" ifadesi büyük ve dönüştürücü bir değişim anlamına gelmekte ve politikacılar ve kitlesel medya satış kampanyaları tarafından sıklıkla abartılı ifadelerle kullanılmaktadır. Kuantum mekaniğinde, bir elektronun bir atomun çekirdeği etrafındaki bir yörüngeden daha yüksek veya daha düşük başka bir yörüngeye geçişini tanımlamak için kullanılır.

Bazen "kuantum" kelimesi ticari ürünlerin ve işletmelerin adlarında kullanılır. Örneğin, Briggs and Stratton çim biçme makineleri, döner çapa makineleri ve diğer küçük makineler için birçok çeşit küçük benzinli motor üretmektedir. Model adlarından biri "Quantum "dur.

Belirsizlik ilkesi bize atomik düzeyde belirli ölçümlerin diğer ölçümleri bozmadan yapılamayacağını söylediği için, bazı kişiler bu fikri insan dünyasında bir gözlemcinin faaliyetinin izlenen şeyi değiştirdiği durumları tanımlamak için kullanır. Bir antropolog, insanların orada nasıl yaşadığını öğrenmek için uzak bir yere gidebilir, ancak dış dünyadan yabancı bir kişinin orada onları izliyor olması, o insanların davranış biçimlerini değiştirebilir.

İnsanların bir şeyleri gözlemlerken yaptıkları ve gözlemleneni değiştiren şeyler Gözlemci etkisi vakalarıdır. İnsanların yaptığı bazı şeyler atomların çok küçük seviyelerinde değişikliklere neden olur ve ilk olarak Heisenberg tarafından tanımlandığı gibi belirsizlik veya belirsizliğin durumlarıdır. Belirsizlik ilkesi, konum ve hız veya yörünge ve momentum gibi belirli ölçüm çiftlerini ne kadar küçük yapabileceğimize dair her zaman bir sınır olduğunu gösterir. Gözlemci etkisi, bazen insanların bir şeyleri gözlemlerken yaptıklarının, örneğin bahçe aletleriyle kazarak bir karınca kolonisi hakkında bilgi edinmenin, öğrenmeye çalıştıkları şeyi değiştiren büyük etkilere sahip olabileceğini söyler.