Planck sabiti

Arka plan

Bu makalede kullanılan semboller.
Sembol Anlamı E Enerji h Planck sabiti k Boltzmann sabiti c ışık hızı λ radyasyon dalga boyu ν radyasyon frekansı T mutlak sıcaklık

1670 ile 1900 yılları arasında bilim insanları ışığın doğasını tartıştılar. Bazı bilim insanları ışığın milyonlarca küçük parçacıktan oluştuğuna inanıyordu. Diğer bilim insanları ise ışığın bir dalga olduğuna inanıyordu.

Işık: dalgalar mı parçacıklar mı?

1678 yılında Christiaan Huygens Traité de la lumiere ("Işık Üzerine İnceleme") adlı kitabı yazdı. Işığın dalgalardan oluştuğuna inanıyordu. Işığın parçacıklardan oluşamayacağını, çünkü iki ışından gelen ışığın birbirlerinden sekmediğini söyledi. 1672'de Isaac Newton Opticks kitabını yazdı. Işığın corpusles adını verdiği kırmızı, sarı ve mavi parçacıklardan oluştuğuna inanıyordu. Newton bunu "iki prizma deneyi" ile açıkladı. İlk prizma ışığı farklı renklere ayırıyordu. İkinci prizma bu renkleri tekrar beyaz ışıkta birleştirdi.

18. yüzyıl boyunca en çok ilgi Newton'un teorisine gösterilmiştir. 1803 yılında Thomas Young "çift yarık deneyini" tanımladı. Bu deneyde, iki dar yarıktan geçen ışık kendisiyle girişim yapar. Bu da ışığın dalgalardan oluştuğunu gösteren bir desene neden olur. On dokuzuncu yüzyılın geri kalanında ışığın dalga teorisi en çok ilgi gören teori oldu. 1860'larda James Clerk Maxwell elektromanyetik radyasyonu dalgalar olarak tanımlayan denklemler geliştirdi.

Elektromanyetik radyasyon teorisi ışığı, radyo dalgalarını, mikrodalgaları ve diğer birçok dalga türünü farklı dalga boylarına sahip olmaları dışında aynı şey olarak ele alır. Gözlerimizle görebildiğimiz ışığın dalga boyu kabaca 400 ila 600 nm arasındadır. Radyo dalgalarının dalga boyu 10 m ila 1500 m arasında değişir ve mikrodalgaların dalga boyu yaklaşık 2 cm'dir. Vakumda tüm elektromanyetik dalgalar ışık hızında hareket eder. Elektromanyetik dalganın frekansı şu şekilde verilir:

ν = c λ {\displaystyle \nu ={\frac {c}{\lambda }}} .

Semboller burada tanımlanmıştır.

Siyah gövde radyatörleri

Sıcak olan her şey elektromanyetik radyasyon olan termal radyasyon yayar. Dünya üzerindeki çoğu şey için bu radyasyon kızıl ötesi aralıktadır, ancak çok sıcak (1000 °C veya daha fazla) bir şey görünür radyasyon, yani ışık yayar. 1800'lerin sonlarında birçok bilim insanı, farklı sıcaklıklardaki kara cisim ışıyıcılarından gelen elektromanyetik radyasyonun dalga boylarını inceledi.

Rayleigh-Jeans Yasası

Lord Rayleigh, Rayleigh-Jeans yasasının temellerini ilk olarak 1900 yılında yayınlamıştır. Teori, gazların kinetik teorisine dayanıyordu. Sir James Jeans 1905 yılında daha kapsamlı bir teori yayınladı. Yasa, farklı sıcaklıklardaki bir siyah cisim radyatörü tarafından yayılan elektromanyetik enerjinin miktarı ve dalga boyu ile ilgilidir. Bunu açıklayan denklem şöyledir:

B λ ( T ) = 2 c k T λ 4 {\displaystyle B_{\lambda }(T)={\frac {2ckT}{\lambda ^{4}}}} .

Uzun dalga boylu radyasyon için, bu denklem tarafından tahmin edilen sonuçlar bir laboratuvarda elde edilen pratik sonuçlarla iyi bir şekilde örtüşmüştür. Ancak, kısa dalga boyları (ultraviyole ışık) için teori ve pratik arasındaki fark o kadar büyüktü ki, "ultra-viyole felaketi" lakabını kazandı.

Planck Yasası

Wien 1895 yılında siyah bir cisimden yayılan radyasyon üzerine yaptığı çalışmaların sonuçlarını yayınladı. Formülü şöyleydi:

B λ ( T ) = 2 h c 2 λ 5 e - h c λ k T {\displaystyle B_{\lambda }(T)={\frac {2hc^{2}}{\lambda ^{5}}e^{-{\frac {hc}{\lambda kT}}}} .

Bu formül kısa dalga boylu elektromanyetik radyasyon için iyi çalışmış, ancak uzun dalga boylarında iyi çalışmamıştır.

1900 yılında Max Planck çalışmalarının sonuçlarını yayınladı. Radyasyonun küçük kuantlardan oluştuğunu varsayarak dalga boyu cinsinden ifade edilen kara cisim radyasyonu için bir ifade geliştirmeye çalıştı ve daha sonra kuantlar sonsuz küçük hale getirilirse ne olacağını görmeye çalıştı (Bu standart bir matematiksel yaklaşımdır). İfade şöyleydi:

B λ ( T ) = 2 h c 2 λ 5 1 e h c λ k T - 1 {\displaystyle B_{\lambda }(T)={\frac {2hc^{2}}{\lambda ^{5}}~{\frac {1}{e^{\frac {hc}{\lambda kT}}-1}}} .

Işığın dalga boyunun çok büyük olmasına izin verilirse, Raleigh-Jeans ve Planck ilişkilerinin neredeyse aynı olduğu gösterilebilir.

h ve k değerlerini hesapladı ve şunu buldu

h = 6,55×10⁻²⁷ erg-sn.

k = 1,34×10⁻¹⁶ erg-deg^-1 .

Değerler, günümüzde kabul edilen sırasıyla 6,62606×10⁻³⁴ ve 1,38065×10⁻¹⁶ değerlerine yakındır. Planck yasası deneysel verilerle uyumludur, ancak tam önemi ancak birkaç yıl sonra anlaşılmıştır.

Işığın kuantum teorisi

Işığın bir eşik frekansına ulaşması durumunda elektronların fotoelektrik etki ile yer değiştirdiği ortaya çıktı. Bunun altında metalden hiçbir elektron yayılamaz. 1905 yılında Albert Einstein bu etkiyi açıklayan bir makale yayınladı. Einstein bir ışık demetinin uzayda yayılan bir dalga olmadığını, daha ziyade her biri enerjiye sahip ayrı dalga paketlerinin (fotonlar) bir koleksiyonu olduğunu öne sürdü. Einstein bu etkinin bir fotonun bir elektrona çarpmasından kaynaklandığını söyledi. Bu, ışığın parçacık doğasını gösteriyordu.

Einstein ayrıca uzun dalga boyuna sahip elektromanyetik radyasyonun hiçbir etkisi olmadığını buldu. Einstein bunun nedeninin "parçacıkların" elektronları rahatsız edecek kadar enerjiye sahip olmaması olduğunu söyledi.

Plank, her bir fotonun enerjisinin foton frekansı ile Planck sabiti arasında bir ilişki olduğunu öne sürmüştür. Bu matematiksel olarak şöyle yazılabilir:

E = h ν = h c λ {\displaystyle E=h\nu ={\frac {hc}{\lambda }}} .

Plank, enerji kuantlarını keşfederek fiziğin ilerlemesine yaptığı hizmetlerden dolayı 1918 yılında Nobel Ödülü'ne layık görülmüştür. Einstein 1921'de Planck sabitini fotoelektrik etkiyle ilişkilendirdiği için Nobel Ödülü aldı.

Newton'un Royal Society'ye yazdığı orijinal mektuptan (1 Ocak 1671 [Jülyen takvimi]) alınan illüstrasyon. S güneş ışığını temsil etmektedir. BC ve DE düzlemleri arasındaki ışık renklidir. Bu renkler yeniden birleşerek GH düzleminde güneş ışığını oluşturur.


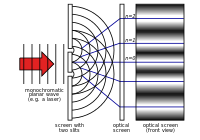
Young'ın çift yarık deneyi


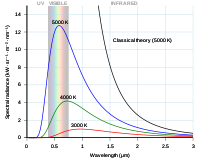
Rayleigh-Jeans eğrisi ve Planck eğrisi foton dalga boyuna karşı çizilmiştir.


Solway Konferansı 1911. Planck, Einstein ve Jeans ayaktalar. Planck soldan ikinci. Einstein sağdan ikinci. Jeans sağdan beşinci. Wien oturuyor, sağdan üçüncü

Uygulama

Planck sabiti birçok uygulamada önem taşımaktadır. Bunlardan birkaçı aşağıda listelenmiştir.

Bohr atom modeli

1913 yılında Niels Bohr, atomun yapısına ilişkin Bohr modelini yayınladı. Bohr, çekirdeğin etrafında dönen elektronların açısal momentumunun sadece belirli değerlere sahip olabileceğini söyledi. Bu değerler şu denklemle verilir

L = n h 2 π {\displaystyle L=n{\frac {h}{2\pi }}}

nerede

L = bir seviye ile ilişkili açısal momentum.

n = pozitif tamsayı.

h = Planck sabiti.

Atomun Bohr modeli, her seviyedeki elektronların enerjisini hesaplamak için kullanılabilir. Elektronlar normalde bir atomun en düşük numaralı durumlarını dolduracaktır. Atom, örneğin bir elektrik akımından enerji alırsa, elektronlar daha yüksek bir duruma uyarılacaktır. Elektronlar daha sonra daha düşük bir duruma geri düşecek ve bir foton yayarak ekstra enerjilerini kaybedeceklerdir. Enerji seviyeleri belirli değerlere sahip olduğundan, fotonlar da belirli enerji seviyelerine sahip olacaktır. Bu şekilde yayılan ışık bir prizma kullanılarak farklı renklere ayrılabilir. Her elementin kendi deseni vardır. Neon için desen yanda gösterilmiştir.

Heisenberg'in belirsizlik ilkesi

1927 yılında Werner Heisenberg belirsizlik ilkesini yayınladı. Bu ilke, ölçülen şeyi bozmadan bir ölçüm yapmanın mümkün olmadığını ifade eder. Ayrıca, bir ölçüm yapmanın neden olduğu minimum rahatsızlığa da bir sınır koyar.

Makroskopik dünyada bu bozulmalar çok az fark yaratır. Örneğin, bir sıvı şişesinin sıcaklığı ölçüldüğünde, termometre ısındıkça az miktarda enerji emecektir. Bu durum son okumada küçük bir hataya neden olacaktır, ancak bu hata küçüktür ve önemli değildir.

Kuantum mekaniğinde işler farklıdır. Bazı ölçümler, saçılan fotonların desenine bakılarak yapılır. Compton saçılması buna bir örnektir. Bir parçacığın hem konumu hem de momentumu ölçülüyorsa, belirsizlik ilkesi momentumun ölçüldüğü doğruluk ile konumun ölçüldüğü doğruluk arasında bir değiş tokuş olduğunu belirtir. Bu değiş tokuşu tanımlayan denklem şöyledir:

Δ x Δ p ≳ h {\displaystyle \Delta x\,\Delta p\gtrsim h\qquad \qquad \qquad }

nerede

Δp = momentumdaki belirsizlik.

Δx = konumdaki belirsizlik.

h = Planck sabiti.

Işık yayan diyotların rengi

Sağda gösterilen elektrik devresinde, ışık yayan diyot (LED) üzerindeki voltaj düşüşü LED'in malzemesine bağlıdır. Silikon diyotlar için bu düşüş 0,6 V iken LED'ler için 1,8 V ile 2,7 V arasındadır. Bu bilgi, bir kullanıcının Planck sabitini hesaplamasını sağlar.

Bir elektronun LED malzemesindeki potansiyel bariyeri atlaması için gereken enerji şu şekilde verilir

E = Q e V L {\displaystyle E=Q_{e}V_{L}\,}

nerede

Q_e bir elektron üzerindeki yüktür.

V_L LED üzerindeki voltaj düşüşüdür.

Elektron tekrar bozunduğunda bir foton ışık yayar. Fotonun enerjisi, fotoelektrik etkide kullanılan aynı denklemle verilir. Bu denklemler birleştirilirse, ışığın dalga boyu ve voltaj şu şekilde ilişkilendirilir

λ = h c V L Q e {\displaystyle \lambda ={\frac {hc}{V_{L}Q_{e}}\,}

Aşağıdaki tablo bu ilişkiden hesaplanabilir.

Renk	Dalga boyu (nm)	Gerilim
kırmızı ışık	650	1.89
yeşil ışık	550	2.25
mavi ışık	470	2.62

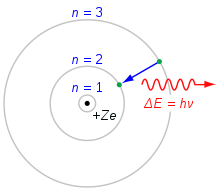
Bohr'un atom modeli. n=3 kabuğundan n=2 kabuğuna düşen bir elektron enerji kaybeder. Bu enerji tek bir foton olarak taşınır.


Neon'un görünür spektrumu. Her çizgi farklı bir enerji seviyesi çiftini temsil eder.


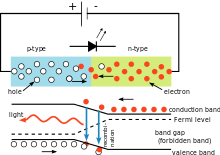
Planck sabitinin kullanımını gösteren basit LED devresi. Yayılan ışığın rengi diyot üzerindeki voltaj düşüşüne bağlıdır. Işığın dalga boyu Planck sabiti kullanılarak hesaplanabilir.

Planck sabitinin değeri ve kilogramın yeniden tanımlanması

Keşfinden bu yana, h ölçümleri çok daha iyi hale gelmiştir. Planck ilk olarak h değerini 6,55×10⁻²⁷ erg-sn olarak vermiştir. Bu değer mevcut değerin %5'i kadardır.

3 Mart 2014 itibariyle SI birimlerinde h değerinin en iyi ölçümü 6.62606957×10⁻³⁴ J-s'dir. Cgs birimlerindeki eşdeğer rakam ise 6.62606957×10⁻²⁷ erg-sn'dir. H'nin bağıl belirsizliği 4.4×10 'dir. ⁻⁸

İndirgenmiş Planck sabiti (ħ) bazen kuantum mekaniğinde kullanılan bir değerdir. Bu değer şu şekilde tanımlanır

ℏ = h 2 π {\displaystyle \hbar ={\frac {h}{2\pi }}} .

Kuantum mekaniğinde bazen SI yerine Planck birimleri kullanılır. Bu sistemde indirgenmiş Planck sabiti 1 değerine sahiptir, dolayısıyla Planck sabitinin değeri 2π'dir.

Plancks sabiti artık çok yüksek hassasiyetle ölçülebilmektedir. Bu durum BIPM'in kilogram için yeni bir tanım düşünmesine neden olmuştur. Uluslararası prototip kilogram artık kilogramı tanımlamak için kullanılmamaktadır. Bunun yerine BIPM, Planck sabitini kesin bir değere sahip olacak şekilde tanımlamaktadır. Bilim adamları kilogramı tanımlamak için bu değeri ve metre ile saniye tanımlarını kullanmaktadır.

 

Teorik Planck sabitinin değeri

Planck sabiti matematiksel olarak da türetilebilir:

 

h = μ 0 π 12 c 3 [ q 0 [ 0,9163 a 0 ] 2 ] 2 f 1 r 5 ⋅ s = 6.63 × 10 - 34 J ⋅ s {\displaystyle h={\frac {\mu _{0}\pi }{12c^{3}}{[{q_{0}}{[0.9163a_{0}]}^{2}]^{2}}{f_{1r}}^{5}\cdot {s}=6.63\times 10^{-34}J\cdot s}

Burada μ 0 {\displaystyle \mu _{0}} serbest uzayın geçirgenliği, c {\displaystyle c} ışık hızı, q 0 {\displaystyle q_{0}} elektronun elektrik yükü, a 0 {\displaystyle a_{0}} Bohr yarıçapı ve f 1 r {\displaystyle f_{1r}} hidrojen atomundaki elektronun dönme frekansıdır ( f 1 r = 3.29 × 10 15 r e v / s ) {\displaystyle (f_{1r}=3.29\times 10^{15}rev/s)} . Bu sabit değerler teorik Planck sabitinde yerine konulduğunda, teorik Planck sabiti değeri deneysel değere tam olarak eşit olmaktadır.

İlgili sayfalar

• Dalga-parçacık ikiliği