Belirsizlik ilkesi

Diyagramlar

1. Fotonlar, elektronlar ve diğer atom altı parçacıklar büyük bir delikten vurulduklarında keskin bir odak noktasına gelirler, ancak yolun tam olarak neresinde olduklarını bilemeyiz.


2. Deliğin daraltılması, parçacıkların yollarını deliğin kenarları etrafında büker (kırınım), böylece ortaya çıkan ışın daha büyük ve yumuşak olur.


3. Deliğin daraltılması fotonun ortada nerede olduğunun kesinliğini artırır, ancak daha sonra oradan sağdaki algılama ekranına olan yönü de buna bağlı olarak daha belirsiz hale gelir. Odak bulanıklaşır. Deliği genişletmek fotonların hepsinin algılama ekranının merkezinde sonlanmasını sağlar, ancak bu durumda merkezi bariyerden geçtiklerinde nerede olduklarına dair daha az fikrimiz olur.


4. Küçük bir deliği olan bir bariyere monte edilen yay, parçacığın delikten geçmesini sağlar, bu da bariyeri iter, yayları gerer ve böylece momentumu ölçer. Ancak yaya monte edilmiş bariyer hareket ettiği için parçacığın delikten geçerken nerede olduğundan daha az emin oluruz ve kırınım da algılama ekranındaki konumunu etkileyecektir.


5. Merkez boşluğu yay ölçekleriyle askıya almak momentumun ölçülmesini sağlar, ancak bunu yapmak boşluğu öngörülemeyen bir şekilde hareket ettirir, böylece her fotonun ortadaki konumu hakkındaki bilgi kaybolur.


6. Bu animasyon evrenin belirsizlik doğasının önemli sonuçlarından birini göstermektedir: elektronların kuantum tünellemesi. Dikkatlice bakın. Her seferinde birazcık bariyeri aşıyor.

İnsanlar belirsizliği nasıl öğrendi?

Werner Heisenberg'in yeni kuantum fiziğini yaratmasından çok kısa bir süre sonra, matematiğinden beklenmedik bir şey çıktı:

Δ x Δ p ≳ h 4 π {\displaystyle \Delta x\,\Delta p\gtrsim {\frac {h}{4\pi }}\qquad \qquad \qquad }

Konumdaki (x) hata aralığı ile momentumdaki (p) hata aralığı çarpımı, Planck sabitinin 4π'ye bölümüne eşit ya da daha büyüktür.

Bu semboller, yukarıdaki resimlerde daha önce gördüğünüz şeyleri matematik formuna sokmaktadır. Bu semboller, bir şeyin nerede olduğu ve nereye gittiği konusunda tam olarak emin olamayacağınızı açık bir şekilde ifade etmektedir. Herhangi bir zamanda nerede olduğu konusunda netleşirseniz, nereye gittiği ve ne kadar hızlı gittiği konusunda daha az fikriniz olur. Herhangi bir zamanda nereye gittiği ve ne kadar hızlı gittiği konusunda netleşirseniz, o zaman şu anda nerede olduğu konusunda daha az fikriniz olur.

Bilim insanları, bazı maddelerin ısıtıldıklarında veya başka bir şekilde uyarıldıklarında neden karakteristik ışık renkleri yaydıklarını zaten öğrenmişlerdi. Heisenberg bu renklerin her birinin neden karakteristik bir parlaklığa sahip olduğunu açıklamaya çalışıyordu. Eğer o ve diğer bilim insanları sadece "Bu iş böyledir" deselerdi bu yeterince iyi olmazdı. Bu farklılıkların ve parlak çizgi güçleri arasındaki oranların bir elementin her örneği için her zaman aynı olmasının iyi bir nedeni olması gerektiğinden emindiler.

Elementlerin her birine özgü renkli çizgilerin yoğunluklarının açıklamasını keşfetmek için yola çıktığında doğanın gizli bir sırrına rastlayacağından habersizdi. Kuantum mekaniği çalışmaları, hidrojenin neden spektrumun insanların görebildiği kısmında dört parlak çizgiye sahip olduğunu zaten göstermişti. Öğrenilmesi gereken bir sonraki şeyin basitçe parlaklıklarının nasıl hesaplanacağı olduğu düşünülmüş olmalı. Hidrojenin uğraşması gereken sadece bir elektronu ve spektrumun görünür kısmında sadece dört çizgisi olduğu için hidrojen başlamak için bariz bir yer gibi görünüyordu. Elbette eşit derecede parlak olmamalarının iyi bir nedeni olmalı. Neon ve diğer elementlerin farklı renkteki çizgilerinin parlaklığının açıklaması bekleyebilirdi.

 

Heisenberg kuantum fiziği üzerinde çalışmaya, başlangıçta çok karmaşık olan elektrik için klasik denklemleri uyarlayarak başladı, bu nedenle 1925 makalesinin arkasındaki matematiği takip etmek çok zordu.

Hidrojen lambası spektrumundaki parlak çizgilerin yoğunluğunu hesaplamak için doğru yolu bulmaya çalışıyordu. İstediği yoğunluğu elde etmek için "genlik" adı verilen ilgili bir niceliği bulması ve genliği genlikle çarpması (ya da başka bir deyişle genliğin karesini alması) gerekiyordu. Genliği, hidrojen lambalarının tüm frekanslarda ışıma yapmadığı ve spektrumun insanların görebildiği kısmında sürekli bir frekans aralığında ışıma yapmadığı gerçeğini hesaba katacak şekilde nasıl ifade edeceğini bulması gerekiyordu. Heisenberg, genliği hesaplamak için dikkate değer yeni bir yol buldu.

Heisenberg'in keşfettiği ve bir kuantum niceliğini (örneğin konum) diğeriyle (örneğin momentum) çarpmak için kullandığı garip denklem, "Heisenberg'in Temmuz 1925 tarihli 'sihirli' makalesi" olarak adlandırılan makalede yayınlandı.

C ( n , n - b ) = ∑ a A ( n , n - a ) B ( n - a , n - b ) {\displaystyle C(n,n-b)=\sum _{a}^{}\,A(n,n-a)B(n-a,n-b)}

Yukarıdaki matematik çok zor görünüyor, ancak buna yol açan matematik çok daha zor ve anlaşılması son derece zor. Burada sadece neye benzediğini göstermek için verilmiştir. Heisenberg'in makalesi tarihi bir dönüm noktasıdır. Makalesini okuyan birçok fizikçi, Heisenberg'in vardığı sonuçlara katılmadıklarını, ancak bu sonuçlara nasıl ulaştığına dair açıklamalarını takip edemediklerini söylemiştir. Heisenberg'in kullandığı başlangıç denklemleri Fourier serilerini içeriyordu ve birçok faktör içeriyordu. Yukarıdaki denkleme geri döneceğiz çünkü matrisleri yazmak ve çarpmak için bir tür reçetedir.

Yeni denklemler çok garip ve alışılmadık olmak zorundaydı çünkü Heisenberg elektronların yörüngeleri gibi bazı şeylerin yavaş yavaş büyümediği ya da küçülmediği garip bir dünyayı tanımlıyordu. Yeni değişim türleri sıçramalar ve sıçramalar arasında büyük boşluklar içerir. Elektronlar yalnızca belirli yörüngeler arasında sıçrayabilir ve yörüngeler arasında geçiş yaparken kazanılan ya da kaybedilen enerji, doğru enerjide bir foton emildiğinde ya da doğru enerjide yeni bir foton üretildiğinde ortaya çıkar. Hidrojen atomlarındaki elektronlar en sık iki belirli yörünge arasında zıplarsa (düşerse), o enerji seviyesinde daha fazla foton yayılır ve böylece o seviyede üretilen ışık en yoğun olur.

Sürekli spektrumlar (güneş ışığını bir prizmadan geçirdiğinizde gördüğünüz şey) için oluşturulmuş denklemleri, aralarında hiçbir şey olmayan sadece birkaç tepe frekansı olan spektrumlara uydurmak zordu. Işık ve enerji hakkında öğrenilen neredeyse her şey yanan mumlar veya güneşler gibi büyük nesnelerle yapılmıştı ve bu büyük nesnelerin hepsi sürekli spektrumlar üretiyordu. Bu sıradan büyüklükteki şeylerle deney yapmak kolay olsa da, onları yöneten yasaları (fizik) bulmak yine de uzun zaman almıştı. Şimdi fizikçiler görülemeyecek kadar küçük, sürekli spektrum üretmeyen şeylerle uğraşıyor ve en azından bildiklerinden bu küçük ve boşluklu ışık kaynaklarının yasalarını bulmalarına yardımcı olacak ipuçları elde etmenin bir yolunu bulmaya çalışıyorlardı.

Orijinal denklemler, bir orgdaki kamışın karakteristik frekansta bir ses dalgası üretmesine benzer şekilde, bir dalga üretecek bir tür titreşen cisimle ilgiliydi. Yani ileri ve geri hareket vardı (bir kamışın titreşimi gibi) ve sinüs dalgası olarak grafiğe geçirilebilecek bir dalga yayılıyordu. Atomik düzeyde fizik hakkında daha önce anlaşılanların çoğu, çekirdeklerin etrafında hareket eden elektronlarla ilgiliydi. Bir kütle bir yörüngede hareket ettiğinde, bir tür merkez etrafında döndüğünde, "açısal momentum" denen şeye sahip olur. Açısal momentum, atlıkarınca gibi bir şeyin, insanlar onu itmeyi bıraktıktan sonra dönmeye devam etmesinin yoludur. Faz hesaplamaları ve açısal momentum için kullanılan matematik karmaşıktır. Üstelik Heisenberg 1925 tarihli makalesinde tüm hesaplamalarını göstermemiştir, bu nedenle iyi matematikçiler bile onun söylemediği şeyleri tamamlamakta zorlanabilir.

Birçok fizikçi Heisenberg'in çığır açan makalesindeki çeşitli matematik adımlarını çözemediklerini söylese de, Heisenberg'in sonuca nasıl ulaştığını açıklamaya çalışan yakın tarihli bir makale yirmi matematik dolu sayfa kullanıyor. Bu makaleyi anlamak bile kolay değil. Matematik gerçekten zor şeylerle başladı ve sonunda bu makalenin başında gösterilen nispeten basit bir şey üretti. Daha basit bir sonuca ulaşmak kolay değildi ve biz de evrenin modası geçmiş bir resminden yeni kuantum fiziğine geçiş sürecini göstermeye çalışmayacağız. Heisenberg buluşunu yapar yapmaz, evrenin işleyişinin daha önce kimsenin görmediği bir parçasının ortaya çıktığını göstermeye yetecek kadar ayrıntıya ihtiyacımız var.

Heisenberg gece geç saatlerde nihayet buluşunu gerçekleştirdiğinde ve bunun işe yarayacağını kendi kendine kanıtlamaya başladığında çok heyecanlı ama aynı zamanda çok yorgun olmalıydı. Neredeyse hemen garip bir şey fark etti, bir şekilde ortadan kaldırabileceği can sıkıcı küçük bir sorun olduğunu düşündüğü bir şey. Ancak bu küçük sıkıntının büyük bir keşif olduğu ortaya çıktı.

Heisenberg genlikleri genliklerle çarpmak için çalışıyordu ve şimdi Heisenberg yeni denklemini kullanarak genliği ifade etmenin iyi bir yoluna sahipti. Doğal olarak çarpma işlemi ve karmaşık denklemler cinsinden verilen şeyleri nasıl çarpacağı hakkında düşünüyordu.

Heisenberg, genliğin karesini almanın yanı sıra, sonunda konumu momentumla çarpmak ya da enerjiyi zamanla çarpmak isteyeceğini fark etti ve bu yeni durumlarda sıralamayı tersine çevirirse bir fark yaratacak gibi görünüyordu. Heisenberg, konumun momentumla mı yoksa momentumun konumla mı çarpıldığının önemli olmaması gerektiğini düşünüyordu. Eğer bunlar sadece basit sayılar olsalardı hiçbir sorun olmazdı. Ancak her ikisi de karmaşık denklemlerdi ve denklemlere girecek sayıları nasıl elde edeceğiniz, hangi yoldan başladığınıza bağlı olarak farklılık gösteriyordu. Doğada önce konumu sonra momentumu ölçmek zorundaydınız ya da önce momentumu sonra konumu ölçmek zorundaydınız ve matematikte de aynı genel durum geçerliydi. (Ayrıntıları öğrenmek istiyorsanız İngilizce Wikipedia'daki Heisenberg'in matris mekaniğine giriş makalesine bakın!) Sonuçlar arasındaki küçük ama sinir bozucu farklar, Heisenberg bunların ortadan kalkmasını ne kadar isterse istesin, kalmaya devam edecekti.

O sırada Heisenberg bu küçük problemden kurtulamamıştı ama çok yorulmuştu, bu yüzden çalışmasını ilk amiri Max Born'a teslim etti ve tatile çıktı.

Max Born, Heisenberg'in kendisine verdiği denklemin bir matris yazmak için bir tür reçete olduğunu kısa sürede gören olağanüstü bir matematikçiydi. Dr. Born, o dönemde çoğu insanın pek bir işe yaramadığını düşündüğü bu tuhaf matematik türüyle ilgilenen az sayıdaki insandan biriydi. Matrislerin çarpılabileceğini biliyordu, dolayısıyla bir fizik probleminin hesaplanmasına yönelik tüm hesaplamalar bir matrisin diğeriyle çarpılmasıyla halledilebilirdi. Karmaşık bir prosedürü standart ve kabul edilebilir bir forma sokabilmek, onunla çalışmayı kolaylaştıracaktı. Ayrıca diğer insanların kabul etmesini de kolaylaştırabilir.

Born o kadar iyi bir matematikçiydi ki, iki matrisin çarpım sırasını değiştirmenin farklı bir sonuç üreteceğini ve sonuçların küçük bir miktar farklı olacağını hemen fark etti. Bu miktar h/2πi olacaktır. Günlük yaşamda bu fark o kadar küçük olurdu ki, bunu göremezdik bile.

Bazı moleküller uyarıldıklarında karakteristik bir renk yayarlar.


Hidrojen spektrumu


Neon spektrumu


Güneşin tam görsel spektrumu. Boşluk yoktur. Bu grafik çeşitli frekanslardaki yoğunlukları göstermektedir.


Birbiriyle aynı fazda olmayan iki dalga

Biçimsel bir belirsizlik teorisine doğru

Birkaç yıl sürdü ama Heisenberg, Δx × Δp = h/2 olduğunu söyleyen Belirsizlik İlkesini kanıtlamayı başardı; bu, orijinal denklemlerden çıkan sayıdır, ancak faz değişiklikleriyle ilgili olan π ve i'yi dışarıda bırakır. Heisenberg, 1927'de bu teoriyi tanıtan bir makale yazdığında belirsizlik ilkesini bu önceki sonuçtan türettiğini açıklamıştır.

Planck sabiti olarak adlandırılan h yazılı sabit, sıklıkla ortaya çıkan gizemli bir sayıdır, bu nedenle bu küçük sayının ne olduğunu anlamamız gerekir. Sayısal olarak genellikle 6,62607×10^-34 J s (joule saniye) olarak verilir. Yani enerji ve zaman içeren bir niceliktir.

Planck, mükemmel bir radyatörün (kara cisim radyatörü olarak adlandırılır) enerjisinin "kuanta" adı verilen belirli büyüklükteki birimler halinde yayıldığını fark ettiğinde keşfedilmiştir (bu kelimenin tekili "kuantum "dur). Yayılan enerji fotonlar olarak yayılır ve bir fotonun frekansı verdiği "yumruk" ile orantılıdır. Görünür ışığın farklı frekanslarını farklı renkler olarak deneyimleriz. Spektrumun mor ucunda her foton nispeten büyük miktarda enerjiye sahiptir; spektrumun kırmızı ucunda ise her foton nispeten küçük miktarda enerjiye sahiptir. Bir fotonun enerji miktarını hesaplamanın yolu E = hν denklemi ile verilir (enerji, Planck sabiti çarpı "nu" veya frekansa eşittir).

Heisenberg belirsizlik ilkesi Δx × Δp ≥ h bize belirli sayı çiftlerini saptamaya çalıştığımızda ancak bu kadar yaklaşabileceğimizi ve bunlardan birini daha netleştirmeye çalışırsak, yani bir şeyin konumu hakkında daha iyi bir fikre sahip olmak için Δx'i küçültmeye çalışırsak, o zaman çiftin diğer sayısı için daha büyük bir sayı geri almamız gerekeceğini ve bu ikisinin sapma miktarının h ile yakından ilişkili olduğunu söyler.

Bir başka fiziksel nicelik çifti de belirsizlik ilişkisine göre ilerler: ΔE × Δt ≥ h ve bu çift, diğer şeylerin yanı sıra, yıldızlararası uzaya, hiçbir şey bulmayı beklemeyeceğimiz bir yere bakarsak ve Δt'yi 0'a yaklaştırırsak, denklemde gösterilen dengeyi korumak için ΔE'nin gittikçe büyümesi gerektiğini gösterir - ve aniden momentumu olan bir şey sadece o kısa süre için ortaya çıkabilir.

Bu belirsizlik (kesinlik eksikliği) nasıl açıklanacaktır? Evrende neler oluyor? Başarılı olan yeni bir teorinin, incelenen olgular hakkında yeni bilgiler sağlayabileceği sıklıkla söylenir. Heisenberg, hidrojenin parlak çizgi spektrumu için doğru yoğunlukları tahmin eden bir matematik modeli yarattı, ancak bunu yapmaya niyetlenmeden, belirli fiziksel nicelik çiftlerinin beklenmedik bir belirsizliği ortaya çıkardığını keşfetti. O ana kadar hiç kimsenin ölçümlerin sonsuza kadar daha kesin ve doğru yapılamayacağı konusunda bir fikri yoktu. Daha kesin, daha kesin hale getirilemeyecekleri gerçeği, çarpıcı yeni bir keşifti. Pek çok insan bunu kabul etmek istemiyordu.

Bohr ve meslektaşları fotonların, elektronların vb. ölçülene kadar konum ya da momentuma sahip olmadıklarını ileri sürmüşlerdir. Bu teorik görüş, belirsizliğin keşfiyle ortaya çıkmıştır ve neye inanılması gerektiğine dair kişisel bir tercih değildir. Bohr, foton ya da elektron gibi bir şey hakkında onu gözlemleyene kadar hiçbir şey bilmediğimizi söyledi. Böylesine küçük bir şeyi gözlemleyebilmek için onunla bir şekilde etkileşime girmemiz gerekir. Günlük yaşamda, bir otomobilin yanında yürürken kaldırıma çizilmiş bir ızgara üzerindeki noktalardan geçtiği zamanları işaretlemek gibi bir şey yapmak mümkündür. Belki de otomobilin ağırlığı kaldırımdaki küçük kollara basarak her birine bağlı saatleri kapatacak ve otomobilin ağırlığını kaydedecektir. Sonunda otomobilin çeşitli zamanlarda nerede olduğuna dair net bir kayda sahip oluruz ve ayrıca ilerleme yönünü ve ağırlığını hesaplayabiliriz. Böylece saatin herhangi bir anında otomobilin hem konumunu hem de momentumunu (hızının kütlesiyle çarpımı) bilebiliriz. Küçük kolları hareket ettirmek için gereken kuvvetin arabanın ilerleyişi üzerinde herhangi bir etkisi olacağını hayal bile edemezdik. Ayrıca otomobilin kaldırım üzerinde kolların bulunduğu noktalar arasında hiçbir konumu ya da yörüngesi olmadığını ya da otomobilin bu süreler boyunca bir tür üç boyutlu bulanıklık içinde var olduğunu ve yalnızca bir kola basarken durulduğunu da hayal edemeyiz. Aşina olduğumuz dünya bu tür garip etkileşimleri ortaya çıkarmaz.

En karanlık gecede denizdeki bir geminin yerini belirlemek için bir projektör kullanabiliriz ve bu ışık geminin konumunu ya da hareket yönünü bozmaz, ancak bir elektronun yerini ışıkla belirlemek için her biri elektronun konumunu ve yörüngesini bozmaya yetecek momentuma sahip bir ya da daha fazla fotonla vurmak gerekir. Elektronun yerini başka yollarla tespit etmek, onu ileri hareketini de sonlandıracak bir tür fiziksel kısıtlama içinde tutmayı gerektirecektir.

Bir fotonun yerini belirlemek için, ileri hareketini sonlandırmadan yapılabilecek en iyi şey, bir bariyerdeki dairesel bir delikten geçmesini sağlamaktır. Fotonun yayıldığı zaman (örneğin bir lazer tarafından) ve fotonun dijital kamera gibi bir algılama ekranına ulaştığı zaman biliniyorsa, bu mesafeyi kat etmek için gereken zamanı ve fotonun delikten geçtiği zamanı hesaplamak mümkündür. Ancak fotonun içinden geçebilmesi için dairesel deliğin çapının fotonun boyutundan daha büyük olması gerekir. Dairesel delik ne kadar küçük yapılırsa, fotonun içinden geçerken tam konumunu bilmeye o kadar yaklaşırız. Ancak, fotonun o anda merkezin dışında olup olmadığını asla bilemeyiz. Eğer delik fotonla tam olarak aynı boyuttaysa, foton içinden geçmeyecektir. Deliğin çapı küçüldükçe, fotonun delikten çıkarkenki momentumu ya da yönü giderek daha büyük ölçüde değişir.

Niels Bohr ve meslektaşları, mikroskopla bile görülemeyecek kadar küçük olan ve sadece günlük yaşam ölçeğinde kanıtlayabildiğimiz şeylerin doğru olduğunu varsayarsak başımızın büyük derde gireceğini ileri sürdüler. Günlük yaşamda her şeyin her zaman belirli bir konumu vardır. Atomik ölçekte ise bu sonucu destekleyecek hiçbir kanıtımız yoktur. Günlük yaşamda, şeylerin meydana geldikleri belirli bir zaman vardır. Atomik ölçekte, bu sonucu destekleyecek hiçbir kanıtımız yoktur. Günlük yaşamda, bir fabrikayı birinci günün gece vardiyasından ikinci günün gündüz vardiyasına kadar gözlemleyen biri, bitmiş bir otomobilin nakliye rıhtımına yuvarlandığını görürse, bunun gece vardiyasında mı yoksa gündüz vardiyasında mı teslim edildiğini söylemenin imkansız olduğunu söylemenin bir anlamı olmayacaktır. Ancak atomik ölçekte, tek bir fotonu iki zamanda üretilmiş olarak saymamız gereken örnekleri gösterebiliriz. (Eğer bu yeterince kötü değilse, tek bir fotonun iki bitişik lazerden üretildiği durumları da gösterebiliriz).

Atomik ölçekte neler olup bittiğini bulmanın zorluklarından biri, bir şeyin hem nerede olduğunu hem de yörüngesinin ne olduğunu bilmek istememiz ve her iki şeyi de aynı anda bilmek istememizdir, ancak hem konumu hem de yörüngeyi aynı anda ölçemeyiz. Ya bir fotonun ya da elektronun momentumunu bir seferde ölçeriz ve daha sonra gereğinden fazla gecikme olmadan konumunu ölçeriz ya da işleri değiştiririz ve önce konumu sonra momentumu ölçeriz. Sorun şu ki, ilkini oldukça kesin bir şekle sokarak (bir şekilde sıkıştırarak) bir sonraki ölçümde yer alan belirsizliği artırıyoruz. Eğer ilk ölçümlerimiz çok kaba olsaydı ve her birinde çok fazla hata olsaydı, o zaman her birini yapmak için daha hafif bir dokunuş kullanarak işleri iyileştirebilirdik, ancak asla belirli bir doğruluk sınırının ötesine geçemezdik.

Günlük hayattan biliyoruz ki, çamaşır makinesinin üzerine yerleştirilmiş bir banyo tartısında bir şeyi tartmaya çalışmak yanlış sonuçlar verecektir, çünkü tartının ibresi kötü bir şekilde sallanacaktır. Çamaşır makinesini kapatabiliriz. Ancak çok hassas ölçümler için mahalleden geçen kamyonların iğneyi oynattığını görürüz, bu nedenle tartıyı dışarıdaki rahatsızlıklardan izole etmek için bir şeyin üzerine koyabiliriz. Titreşimleri istediğimiz kadar doğru sonuçlar verecek kadar ortadan kaldırabileceğimize inanıyoruz. Tartının üzerindeki şeyin kendisinin de titreştiğini ya da belirsiz bir momentuma sahip olduğunu asla düşünmeyiz.

Belirsizlik İlkesi'nden geriye doğru gidildiğinde, atomik ölçekteki herhangi bir şey için aslında kesin bir konum ve kesin bir momentum olmadığı ve deneycilerin yalnızca Belirsizlik İlkesi tarafından belirtilen sınır dahilinde şeyleri kesinliğe zorlayabileceği görülmektedir. Bohr ve meslektaşları sadece ölçümler yapmadan hiçbir şey bilemeyeceğimizi ve ölçümler yapıldığında şeyleri daha kesin konum veya daha kesin momentum yönünde zorlayabileceğimizi, ancak istediğimiz mutlak kesinliği veya kesinliği elde edemeyeceğimizi savundular. Ancak diğerleri bu olasılığı ciddiye aldı ve eğer matematik doğruysa o zaman ultra küçük dünyada kesinlik ya da belirlilik olamayacağını savundu. Bilimin doğası gereği matematik sadece gerçekliğin bir modelidir ve bunun doğru bir model olduğunun garantisi yoktur.

Matematik ve matematiğin öngördüğü şeylerin pratik sonuçları o kadar güvenilirdir ki bunlara karşı çıkmak çok zordur, ancak matematiğin gerçek dünya hakkında söyledikleri birkaç farklı fikir üretmiştir. Kopenhag'da Niels Bohr ile çalışan bilim insanları arasında belirsizlik ilkesi, temel düzeyde fiziksel evrenin deterministik bir biçimde var olmadığı anlamına geliyordu. Aksine, bir olasılıklar ya da potansiyeller bütünüdür.

Kopenhag grubu tarafından matematik etrafında örülen hikayeye karşı, kuantum teorisine göre birden fazla olası sonuç olduğunda, her sonucun kendi yeni evreninde meydana geldiğini söyleyen "çoklu evrenler yorumu" gibi başka hikayeler de vardır. Einstein birden fazla olası sonuç olmadığını, dolayısıyla tek bir evren olduğunu ve bunun da belirli olduğunu ya da kendi deyimiyle "Tanrı'nın zar atmadığını" savunmuştur.

Eğer h mümkün olan en küçük enerji miktarı olsaydı, çeşitli frekanstaki fotonların içerdiği enerjiyi gösteren temel denklem dengede olmazdı. Yanlış olurdu.

Belirsizlik ilkesine karşı itirazlar

Albert Einstein yeni kuantum mekaniğinin, ölçümlerin yapılmasından önceki zamanda konum ve momentum eksikliğini ima ettiğini gördü ve buna şiddetle itiraz etti. Şeylerin ölçülmeden önce belirli konumlara ve belirli momentumlara sahip olduğuna ve bir çift şeyden birini ölçmenin diğerini doğru bir şekilde ölçme olasılığını bozmasının, bunlardan herhangi birinin önceden eksik olduğunu iddia etmediğine kesinlikle inanıyordu. O ve iki meslektaşı "EPR makalesi" olarak bilinen makaleyi yazdılar. Bu makale, konum ve momentumu belirleyen özellikler olması gerektiğini ve eğer bunları görebilirsek ya da bunlar hakkında bilgi edinebilirsek, o zaman matematiksel olarak konum ve momentumu bilebileceğimizi ve tahmin edebileceğimizi savunmaktadır. Uzun bir süre boyunca insanlar Einstein için bir inanç maddesi olan şeyi kanıtlamanın ya da çürütmenin hiçbir yolu olmadığını düşündüler. Bu tartışma çok verimli oldu çünkü dolaşıklık konusundaki tüm modern gelişmelere yol açtı.

Matematiksel olarak Einstein'ın yanıldığı kanıtlandı. 1964 yılında John Stewart Bell, sadece onları inceleyen iki kişi tarafından bilinmeyen belirli durumlara sahip iki parçacık ile ölçülene kadar belirsiz veya belirsiz olan dolaşık durumlara sahip iki parçacığın davranışını ayırt etmek için bir matematik yöntemi geliştirdi. Yöntemi, iki farklı varsayım altında belirli sonuçlara ulaşma olasılıklarının farklı olduğunu göstermektedir. Çalışması Bell teoremi veya Bell Eşitsizliği olarak adlandırılır. Deneyler, doğanın Bell'in tanımladığı gibi davrandığını göstermiştir.

Belirsizliğe giden başka bir yol

Heisenberg'in belirsizlik ilkesinin ilk tartışmaları, elektronlar, protonlar vb. gibi madde parçacıklarının bir dalga boyuna sahip olduğunu dikkate almayan bir modele dayanıyordu. 1926'da Louis de Broglie, sadece fotonların değil, her şeyin kendi frekansı olduğunu gösterdi. Tıpkı fotonlar gibi her şeyin bir dalga doğası ve bir parçacık doğası vardır. Proton gibi bir şeyin dalgasını daha dar ve daha uzun yapmaya çalışırsak, bu onun konumunu daha net hale getirecektir, ancak o zaman momentum daha az iyi tanımlanacaktır. Bir dalga tanımının momentum kısmını daha net hale getirmeye çalışırsak, yani daha dar bir değer aralığında kalmasını sağlarsak, o zaman dalga tepe noktası yayılır ve konumu daha az belirgin hale gelir.

Kuantum mekaniğinde foton tanımının bir parçası olan dalga, okyanus yüzeyindeki dalgayla ya da ses dalgalarını oluşturan sıkıştırılmış hava ve seyreltik hava bölgeleriyle aynı türden bir şey değildir. Bunun yerine, bu dalgaların uzay ve zamanda o noktada bir şey bulma olasılığı ile ilgili tepe noktaları veya yüksek genlikli bölgeleri vardır. Daha doğrusu, bazı fenomenlerin ortaya çıkma olasılığını veren genliğin karesidir.

Bir foton için geçerli olan dalga saf bir sinüs dalgası olabilir. Bu durumda, her tepe noktasının değerinin karesi, fotonun o noktada gözlemlenme olasılığını verecektir. Sinüs dalgalarının genlikleri her yerde aynı olduğundan, fotonu her birinde bulma olasılığı da aynı olacaktır. Dolayısıyla, pratik olarak konuşmak gerekirse, bu fotonlardan biri için dalgayı bilmek, onu nerede arayacağımız konusunda bir ipucu vermeyecektir. Öte yandan, bir fotonun momentumu matematiksel olarak dalgasının genliği ile ilişkilidir. Bu durumda saf bir sinüs dalgasına sahip olduğumuzdan, dalganın her döngüsünün genliği aynıdır ve bu nedenle bu dalgayla ilişkili yalnızca bir momentum değeri vardır. Fotonun nereye çarpacağını bilemeyiz ama tam olarak ne kadar sert çarpacağını biliriz.

Bir algılama ekranı üzerindeki bir noktaya odaklanan ışık demetlerinde, fotonlarla ilişkili dalgalar saf sinüs dalgaları değildir. Bunun yerine, bir noktada yüksek genlikli ve bu en yüksek tepe noktasının her iki yanında çok daha düşük genlikli dalgalardır. Matematiksel olarak böyle bir dalgayı farklı dalga boylarına sahip bir dizi farklı sinüs dalgası olarak analiz etmek mümkündür. Bu sürecin tersini, bir frekanstaki ilk sinüs dalgasına bakarak görselleştirmek biraz daha kolaydır, buna farklı bir dalga boyunda ikinci bir sinüs dalgası, sonra bir üçüncüsü, sonra bir dördüncüsü ve bu şekilde devam eder. Sonuç, yüksek bir tepe noktası gösteren ve farklı dalga boylarında ve dolayısıyla farklı momentumlarda çok sayıda dalga içeren karmaşık bir dalga olacaktır. Bu durumda, fotonun belirli bir noktada ortaya çıkma olasılığı son derece yüksektir, ancak sağladığı momentum, bileşen dalgalardan herhangi birinin dalga boyuyla ilişkili olabilir. Başka bir deyişle, p = ħ/λ değeri artık tek bir değer değildir, çünkü bir araya getirilen "farklı dalga boyundaki dalgaların" tüm uzunluklarının hesaba katılması gerekir.

Simülasyon, bir parçacığın konumunun keskinleşmesinin matematiksel olarak nasıl modelleneceğini göstermektedir: Orijinal sinüs dalgasının üzerine birçok farklı dalga formu yerleştirin. Merkez giderek daha yüksek bir tepe oluşturacak ve geri kalan tepelerin sayısı artacak ancak birbirleriyle etkileşime girecekleri için yükseklikleri azalacaktır. Sonuçta süperpozisyonda her biri farklı bir dalga boyuna ve (p = ħ/λ ile) farklı bir momentuma sahip birçok farklı dalga vardır, ancak yalnızca çok yüksek bir tepe vardır, bu tepe gittikçe yükselir ve daralır ve bize belirli bir konuma gittikçe daha yakın bir şey verir.

Momentumu gittikçe daha belirgin hale getirmek için, elimizde sadece basit bir sinüs dalgası kalana kadar üst üste binmiş sinüs dalgalarını gittikçe daha fazla almamız gerekecektir. Bunu yaparken merkezi tepe noktasının yüksekliğini giderek azaltır ve parçacığın bulunabileceği rakip yerlerin yüksekliklerini giderek arttırırdık.

Dolayısıyla, atom altı parçacıkların dalga resmiyle başladığımızda, tipik olarak her zaman nispeten uzun merkezi tepe noktaları ve nispeten çok sayıda bileşen dalga boyu olan durumlarla ilgileneceğiz. Bu koşullar altında hiçbir zaman kesin bir konum ya da kesin bir momentum öngörülmeyecektir. Eğer matematiksel model gerçek dünyanın doğru bir temsiliyse, o zaman hiçbir foton ya da diğer atomaltı parçacık kesin bir konuma ya da kesin bir momentuma sahip değildir. Böyle bir parçacığı ölçtüğümüzde, tepe noktasını daha da sıkıştıran ve daraltan bir yöntem seçebiliriz ya da tepe noktasını alçaltan ve bileşen dalga boylarını eşitleyen bir yöntem seçebiliriz. Neyi ölçtüğümüze ve nasıl ölçtüğümüze bağlı olarak, konumumuzu daha kesin hale getirebilir veya momentum aralığımızı daraltabiliriz. Deneyi tasarlarken aygıtı çeşitli şekillerde oynatmaktan kaçınmaya özen gösterebiliriz, ancak başlangıçta hiçbir şeyin tam olarak kesin olmadığı gerçeğinden kurtulamayız.

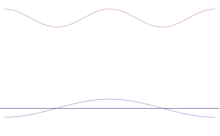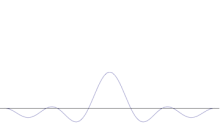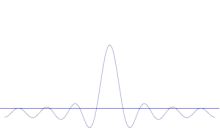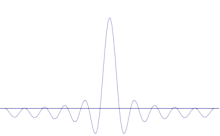
Birkaç düzlem dalganın süperpozisyonu. Dalga paketi, birçok dalganın eklenmesiyle giderek yerelleşir. Fourier dönüşümü, bir dalga paketini bireysel düzlem dalgalarına ayıran matematiksel bir işlemdir. Burada gösterilen dalgaların sadece açıklama amacıyla gerçek olduğunu, oysa kuantum mekaniğinde dalga fonksiyonunun genellikle karmaşık olduğunu unutmayın.

Kültürel etkiler

Heisenberg Belirsizlik İlkesi'nin en önemli etkisi, irade özgürlüğüne ilişkin tartışmalar üzerinde olmuştur. Klasik fizik teorileri altında, neden ve sonuç yasalarının amansız olduğunu ve evren bir kez belirli bir şekilde başladığında, gelecekte meydana gelecek tüm madde ve enerji etkileşimlerinin bu başlangıç durumundan hesaplanabileceğini iddia etmek mümkündür. Her şey kesinlikle kendisinden önce gelenlerin sonucu olduğu için, bir insanın verdiği her kararın ve içine girdiği her durumun zamanın başlangıcından beri önceden belirlenmiş olduğunu savunmuşlardır. O halde ne yapacağımıza dair hiçbir seçeneğimiz yoktur.

İrade özgürlüğüne inanan insanlar, kuantum mekaniği yasalarının ne olacağını değil, sadece neyin daha fazla neyin daha az gerçekleşme olasılığı olduğunu öngördüğünü savunurlar. Dolayısıyla her eylem bir dizi rastgele "yazı tura "nın sonucudur ve hiçbir karar bir dizi gerekli önkoşula dayandırılamaz.

"Kuantum sıçraması" ve "kuantum sıçraması" ifadeleri, bir şeyler hakkında konuşmanın sıradan yolları haline geldi. Genellikle insanlar bir şeyi kısa bir süre içinde meydana gelen büyük bir değişim olarak tanımlamayı amaçlarlar. Bu terim aslında bir elektronun bir atomda ya dışarıdan gelen bir fotonu emdiğinde ve böylece atomun çekirdeği etrafındaki bir yörüngeden daha yüksek bir yörüngeye sıçradığında ya da bir foton yaydığında ve böylece daha yüksek bir yörüngeden daha düşük bir yörüngeye düştüğünde nasıl davrandığı için geçerlidir. Neils Bohr ve meslektaşlarının fikri, elektronun yörüngeler arasında hareket etmediği, bunun yerine bir yörüngeden kaybolduğu ve anında başka bir yörüngede belirdiği yönündeydi. Yani kuantum sıçraması gerçekten de dünyayı sarsan bir değişim değil, bir alandan diğerine ani küçük bir değişimdir.

İnsanlar atom altı ölçekte bir süreci ölçtüğünde ve belirsizlik ilkesi kendini gösterdiğinde, insan eyleminin ölçülen şeyi etkilediği söylenebilir. Bir parçacığın konumunun kesin bir göstergesini elde etmek amacıyla bir ölçüm yapmak kaçınılmaz olarak momentumunu etkileyecektir ve konumunu ölçtükten sonra mümkün olan en kısa sürede bu momentumu ölçmek için ne yapılırsa yapılsın, hangi momentumun keşfedileceğine dair olasılıkların değişmiş olması kaçınılmazdır. Dolayısıyla belirsizlik ilkesi, araştırmacılar tarafından üretilen ve bir deneyin ya da gözlemin sonuçlarını etkileyen bazı girişim türlerini açıklayabilir. Ancak gözlemci etkilerinin tümü kuantum etkilerinden ya da belirsizlik ilkesinden kaynaklanmaz. Geri kalanlar "gözlemci etkileridir" ancak kuantum belirsizlik etkileri değildir.

Gözlemci etkileri, sıradan insani olay ölçeğimizde işleyen her türlü şeyi içerir. Eğer bir antropolog ilkel bir toplumdaki yaşam hakkında net bir fikir edinmeye çalışıyorsa, ancak varlığı ziyaret ettiği topluluğu rahatsız ediyorsa, yapılan gözlemler çok yanıltıcı olabilir. Bununla birlikte, ilgili etkileşimlerin hiçbiri kuantum mekaniği veya belirsizlik ilkesi tarafından tanımlanan düzeyde gerçekleşmez.

Bazen "kuantum" kelimesi yeni ve güçlü bir şeyi belirtmek için reklam amaçlı kullanılır. Örneğin, küçük benzinli motor üreticisi Briggs and Stratton, benzinli çim biçme makineleri ve benzer bahçe aletleri için "Quantum" adını verdiği dört silindirli düşük beygir gücünde bir motor serisine sahiptir.

Daha fazla okuma

• Kuantum Teorisine Giriş, s. 115 ve s. 158

J.P. McEvoy ve Oscar Zarate