Altın Oran
Bir a sayısı ve daha küçük başka bir b sayısı ile, iki sayının oranı onları bölerek bulunur. Oranları a/b'dir. İki sayıyı toplayarak başka bir oran bulunur a+b ve bunu daha büyük olan a sayısına bölerek yeni oran (a+b)/a'dır. Bu iki oran aynı sayıya eşitse, o sayıya altın oran denir. Yunan harfi φ {\displaystyle \varphi } 
(phi) genellikle altın oranın adı olarak kullanılır.
Örneğin, b = 1 ve a/b = φ {\displaystyle \varphi } ise , o zaman a = φ {\displaystyle \varphi } . İkinci oran (a+b)/a ise ( φ + 1 ) / φ {\displaystyle (\varphi +1)/\varphi } şeklindedir. 
. Bu iki oran eşit olduğu için bu doğrudur:
φ = φ + 1 φ {\displaystyle \varphi ={\frac {\varphi +1}{\varphi }}
Bu sayıyı yazmanın bir yolu şudur
φ = 1 + 5 2 {\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}}
5 {\displaystyle {\sqrt {5}}}
kendisiyle çarpıldığında 5 yapan herhangi bir sayı gibidir (veya hangi sayı çarpılırsa çarpılsın): 5 × 5 = 5 {\displaystyle {\sqrt {5}}\times {\sqrt {5}}=5}
.
Altın oran irrasyonel bir sayıdır. Bir kişi onu yazmaya çalışırsa, asla durmayacak ve asla bir desen oluşturmayacaktır, ancak şu şekilde başlayacaktır: 1.6180339887... Bu sayıyla ilgili önemli bir şey, bir kişinin ondan 1 çıkarabilmesi veya 1'i ona bölebilmesidir. Her iki durumda da sayı devam edecek ve asla durmayacaktır.
Altın dikdörtgen
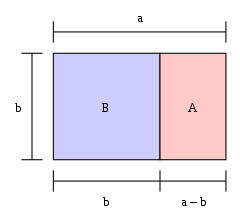
Bir dikdörtgenin uzunluğunun genişliğine bölümü altın orana eşitse, o dikdörtgen bir "altın dikdörtgen "dir. Bir altın dikdörtgenin bir ucundan bir kare kesilirse, diğer uç yeni bir altın dikdörtgendir. Resimde, büyük dikdörtgen (mavi ve pembe birlikte) bir altın dikdörtgendir çünkü a / b = φ {\displaystyle a/b=\varphi } 
. Mavi kısım (B) bir karedir. Pembe kısım tek başına (A) başka bir altın dikdörtgendir çünkü b / ( a - b ) = φ {\displaystyle b/(a-b)=\varphi } 
. Büyük dikdörtgen ve pembe dikdörtgen aynı biçime sahiptir, ancak pembe dikdörtgen daha küçüktür ve döndürülmüştür.
Büyük dikdörtgen BA bir altın dikdörtgendir; yani b:a oranı 1'dir: φ {\displaystyle \varphi } . Bu tür herhangi bir dikdörtgen için ve sadece bu belirli orandaki dikdörtgenler için, B karesini çıkarırsak, geriye kalan A, başka bir altın dikdörtgendir; yani orijinal dikdörtgenle aynı oranlara sahiptir.
Fibonacci sayıları
Fibonacci sayıları bir sayı listesidir. Bir kişi listedeki bir sonraki sayıyı son iki sayıyı toplayarak bulabilir. Eğer bir kişi listedeki bir sayıyı kendisinden önce gelen sayıya bölerse, bu oran giderek altın orana yaklaşır.
| Fibonacci sayısı | bir öncekine bölünür | oran |
| 1 | ||
| 1 | 1/1 | = 1.0000 |
| 2 | 2/1 | = 2.0000 |
| 3 | 3/2 | = 1.5000 |
| 5 | 5/3 | = 1.6667 |
| 8 | 8/5 | = 1.6000 |
| 13 | 13/8 | = 1.6250 |
| 21 | 21/13 | = 1.6154... |
| 34 | 34/21 | = 1.6190... |
| 55 | 55/34 | = 1.6177... |
| 89 | 89/55 | = 1.6182... |
| ... | ... | ... |
| φ {\displaystyle \varphi } | = 1.6180... |
Doğada altın oran
Doğada altın oran genellikle yaprakların veya çiçeklerin düzenlenmesi için kullanılır. Bunlar yaklaşık 137,5 derecelik altın açıyı kullanır. Bu açıda düzenlenmiş yapraklar veya çiçekler güneş ışığını en iyi şekilde kullanır.
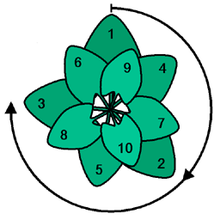
Altın açıyı kullanmak güneş ışığını en iyi şekilde kullanacaktır. Bu tepeden bir görünüm.
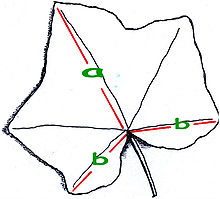
Altın oranı gösteren bir sarmaşık yaprağı
Sorular ve Yanıtlar
S: İki sayının oranı nedir?
C: İki sayının oranı onları bölerek bulunur, bu nedenle oran a/b olacaktır.
S: Başka bir oran nasıl bulunabilir?
C: Başka bir oran, iki sayıyı toplayarak ve daha sonra bu toplamı büyük sayı olan a'ya bölerek bulunabilir. Bu yeni oran (a+b)/a olacaktır.
S: Bu iki oranın birbirine eşit olduğu duruma ne ad verilir?
C: Bu iki oran birbirine eşit olduğunda buna altın oran denir. Genellikle Yunan harfi צ veya phi ile gösterilir.
S: Eğer b = 1 ve a/b = צ ise, bu a için ne anlama gelir?
C: Eğer b = 1 ve a/b = צ ise, bu a = צ anlamına da gelir.
S: Bu sayı nasıl yazılabilir?
C: Bu sayıyı yazmanın bir yolu צ = 1 + 5 / 2 = 1.618'dir...
S: Bu sayıdan 1 çıkarırsanız veya 1'i bölerseniz ne anlama gelir?
C: Ondan 1 çıkarırsanız veya 1'i ona bölerseniz, aynı sayıyı geri alırsınız - başka bir deyişle, her ikisi de altın orana eşit olur.
S: Altın oran irrasyonel bir sayı mıdır?
C: Evet, altın oran irrasyonel bir sayıdır, yani birisi onu yazmaya çalışırsa, asla bir sonu ve kalıbı olmayacaktır - sadece "1.6180339887..." gibi bir şeyle başlayacaktır.
