Yüzey gerilimi
Yüzey gerilimi, bir sıvının yüzeyinin güçlü olduğu bir etkidir. Yüzey bir ağırlığı tutabilir ve bir su damlacığının yüzeyi damlacığı bir top şeklinde bir arada tutar. Bazı küçük cisimler normalde yüzemeyecekleri halde yüzey gerilimi nedeniyle bir yüzey üzerinde yüzebilirler. Bazı böcekler (örneğin suda yürüyenler) bu sayede su yüzeyinde koşabilirler. Bu özellik, sıvıdaki moleküllerin birbirini çekmesinden (kohezyon) kaynaklanır ve sıvıların birçok davranışından sorumludur.
Yüzey gerilimi, birim uzunluk başına kuvvet veya birim alan başına enerji boyutuna sahiptir. Bu ikisi eşdeğerdir ancak birim alan başına düşen enerjiden bahsederken insanlar yüzey enerjisi terimini kullanırlar ki bu sadece sıvılar için değil katılar için de geçerli olması anlamında daha genel bir terimdir.
Malzeme biliminde yüzey gerilimi, yüzey gerilimi ya da yüzey serbest enerjisi için kullanılır.
Nedenler
Sıvı molekülleri arasındaki kohezif kuvvetler yüzey gerilimine neden olur. Sıvının büyük kısmında, her bir molekül komşu sıvı molekülleri tarafından her yönde eşit olarak çekilir ve net kuvvet sıfır olur. Yüzeydeki moleküllerin her tarafında başka moleküller bulunmaz ve bu nedenle içe doğru çekilirler. Bu durum bir miktar iç basınç yaratır ve sıvı yüzeylerini minimum alana kadar daralmaya zorlar.
Sıvı damlacıklarının şeklinden yüzey gerilimi sorumludur. Kolayca deforme olabilmesine rağmen, su damlacıkları yüzey tabakasının yapışkan kuvvetleri tarafından küresel bir şekle çekilme eğilimindedir. Yerçekimi de dahil olmak üzere diğer kuvvetlerin yokluğunda, neredeyse tüm sıvıların damlaları mükemmel bir şekilde küresel olacaktır. Küresel şekil, Laplace yasasına göre yüzey tabakasının gerekli "duvar gerilimini" en aza indirir.
Bunu enerji açısından görmenin başka bir yolu da var. Bir komşusuyla temas halinde olan bir molekül, tek başına (komşusuyla temas halinde olmayan) bir moleküle göre daha düşük bir enerji durumundadır. İç moleküller sahip olabilecekleri kadar çok komşuya sahiptir, ancak sınır moleküllerinin komşuları eksiktir (iç moleküllere kıyasla). Dolayısıyla, sınır molekülleri daha yüksek enerjiye sahiptir. Sıvının enerji durumunu minimize etmesi için, daha yüksek enerjili sınır moleküllerinin sayısının minimize edilmesi gerekir. En aza indirgenmiş sınır molekülü miktarı, en aza indirgenmiş yüzey alanı ile sonuçlanır.
Yüzey alanı minimizasyonunun bir sonucu olarak, bir yüzey alabileceği en düzgün şekli alacaktır. Yüzey şeklindeki herhangi bir eğrilik daha büyük bir alan ve daha yüksek bir enerji ile sonuçlanır. Dolayısıyla yüzey, tıpkı yokuş yukarı itilen bir topun yerçekimsel potansiyel enerjisini en aza indirmek için geri itilmesi gibi herhangi bir eğriliğe karşı geri itilecektir.
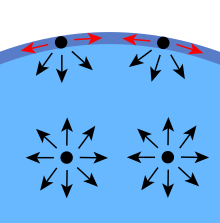
Sıvı içindeki moleküller üzerindeki kuvvetlerin diyagramı

Yüzey gerilimi ataşın suya batmasını engeller.
Günlük yaşamdaki etkileri
Su
Suyun incelenmesi, yüzey geriliminin çeşitli etkilerini göstermektedir:
A. Yağmur suyu, yaprak gibi mumsu bir yüzeyin yüzeyinde boncuklar oluşturur. Su balmumuna zayıf, kendisine ise güçlü bir şekilde yapışır, bu nedenle su damlalar halinde kümelenir. Yüzey gerilimi onlara küreye yakın bir şekil verir, çünkü bir küre mümkün olan en küçük yüzey alanı/hacim oranına sahiptir.
B. Damla oluşumu, bir sıvı kütlesi gerildiğinde meydana gelir. Animasyon, yüzey geriliminin artık onu musluğa bağlayamayacağı bir noktaya kadar gerilene kadar musluğa yapışan suyun kütle kazandığını göstermektedir. Daha sonra ayrılır ve yüzey gerilimi damlayı bir küre haline getirir. Musluktan bir su akışı olsaydı, akış düşüşü sırasında damlalara ayrılırdı. Yerçekimi akışı gerer, ardından yüzey gerilimi onu küreler halinde sıkıştırır.
C. Sudan daha yoğun cisimler, cisim ıslanmadığında ve ağırlığı yüzey geriliminden kaynaklanan kuvvetler tarafından taşınabilecek kadar küçük olduğunda yine de yüzer. Örneğin, su cambazları bir göletin yüzeyinde yürümek için yüzey gerilimini kullanırlar. Suyun yüzeyi elastik bir film gibi davranır: böceğin ayakları suyun yüzeyinde girintilere neden olarak yüzey alanını artırır.
D. Yağ ve suyun (bu durumda su ve sıvı balmumu) ayrılması, birbirine benzemeyen sıvılar arasındaki yüzey geriliminden kaynaklanır. Bu tür yüzey gerilimine "arayüzey gerilimi" denir, ancak fiziği aynıdır.
E. Şarap gözyaşları, alkollü bir içecek içeren bir bardağın kenarında damlalar ve perçemler oluşmasıdır. Bunun nedeni su ve etanolün farklı yüzey gerilimleri arasındaki karmaşık etkileşimdir. Etanolün sudan daha hızlı buharlaşmasıyla birlikte suyun yüzey geriliminin etanol tarafından değiştirilmesinin bir kombinasyonu ile indüklenir.
· 
A. Yaprak üzerinde su damlacıkları
· 
B. Musluktan damlayan su
· 
C. Su striderları yüzey gerilimi nedeniyle sıvının üstünde kalır
· 
D. Birbirine benzemeyen sıvılar arasında etkileşim olan lav lambası; su ve sıvı balmumu
· 
E. "Şarap gözyaşları" fenomenini gösteren fotoğraf.
Yüzey Aktif Maddeler
Yüzey gerilimi, özellikle azaltmak için yüzey aktif maddeler kullanıldığında, diğer yaygın olaylarda görülebilir:
- Sabun baloncukları çok az kütleye sahip çok geniş yüzey alanlarına sahiptir. Saf su içindeki kabarcıklar kararsızdır. Ancak yüzey aktif maddelerin eklenmesi kabarcıklar üzerinde dengeleyici bir etkiye sahip olabilir (bkz. Marangoni etkisi). Yüzey aktif maddelerin aslında suyun yüzey gerilimini üç veya daha fazla kat azalttığına dikkat edin.
- Emülsiyonlar, yüzey geriliminin rol oynadığı bir çözelti türüdür. Saf su içinde asılı duran küçük yağ parçaları kendiliğinden çok daha büyük kütleler halinde bir araya gelecektir. Ancak bir yüzey aktif maddenin varlığı, yüzey geriliminde bir azalma sağlar ve bu da küçük yağ damlacıklarının su kütlesi içinde stabilitesine izin verir (veya tam tersi).
Temel fizik
İki tanım
γ sembolü ile temsil edilen yüzey gerilimi, kuvvetin yüzeye paralel ancak çizgiye dik olduğu birim uzunluktaki bir çizgi boyunca kuvvet olarak tanımlanır. Bunu resmetmenin bir yolu, bir tarafı L uzunluğunda gergin bir iplikle sınırlanmış düz bir sabun filmi hayal etmektir. 
Termodinamikte kullanışlı olan eşdeğer bir tanım, birim alan başına yapılan iştir. Bu nedenle, bir sıvı kütlesinin yüzey alanını bir miktar, δA, artırmak için bir miktar iş, γ {\displaystyle \scriptstyle \gamma } 
Birim alan başına enerji ölçümünün birim uzunluk başına kuvvet ölçümüne eşdeğerliği boyutsal analiz ile kanıtlanabilir.
Yüzey eğriliği ve basınç
Gerilmiş bir yüzeye hiçbir kuvvet normal etki etmiyorsa, yüzey düz kalmalıdır. Ancak yüzeyin bir tarafındaki basınç diğer tarafındaki basınçtan farklıysa, basınç farkı çarpı yüzey alanı normal bir kuvvetle sonuçlanır. Yüzey gerilim kuvvetlerinin basınçtan kaynaklanan kuvveti iptal etmesi için yüzeyin kavisli olması gerekir. Diyagram, küçük bir yüzey parçasının yüzey eğriliğinin, parçanın merkezine normal etki eden yüzey gerilim kuvvetlerinin net bir bileşenine nasıl yol açtığını göstermektedir. Tüm kuvvetler dengelendiğinde, ortaya çıkan denklem Young-Laplace denklemi olarak bilinir:
Δ p = γ ( 1 R x + 1 R y ) {\displaystyle \Delta p\ =\ \gamma \left({\frac {1}{R_{x}}+{\frac {1}{R_{y}}}\right)}
Nerede?
· Δp basınç farkıdır.
· γ {\displaystyle \scriptstyle \gamma }
· Rx ve Ry yüzeye paralel olan eksenlerin her birindeki eğrilik yarıçaplarıdır.
Sağ taraftaki parantez içindeki miktar aslında (normalleştirmeye bağlı olarak) yüzeyin ortalama eğriliğidir (iki katı).
Bu denklemin çözümleri su damlalarının, su birikintilerinin, menisküslerin, sabun baloncuklarının ve yüzey gerilimi tarafından belirlenen diğer tüm şekillerin şeklini belirler. (Bir başka örnek de bir su yürüyüşçüsünün ayaklarının gölet yüzeyinde bıraktığı izlerin şeklidir).
Aşağıdaki tablo, bir su damlacığının iç basıncının azalan yarıçapla nasıl arttığını göstermektedir. Çok küçük olmayan damlalar için bu etki hafiftir, ancak damla boyutları moleküler boyuta yaklaştığında basınç farkı muazzam hale gelir. (Tek bir molekül sınırında bu kavram anlamsız hale gelir).
| STP'de farklı yarıçaplı su damlaları için Δp | ||||
| Damlacık yarıçapı | 1 mm | 0,1 mm | 1 μm | 10 nm |
| Δp (atm) | 0.0014 | 0.0144 | 1.436 | 143.6 |
Sıvı yüzey
Keyfi şekilli bir çerçeve tarafından sınırlanan minimal yüzeyin şeklini sadece matematik kullanarak bulmak zordur. Yine de çerçeveyi telden şekillendirip sabun çözeltisine daldırdığınızda, ortaya çıkan sabun filminde saniyeler içinde yerel olarak minimal bir yüzey belirecektir.
Bunun nedeni, Young-Laplace denkleminde görüldüğü gibi, bir akışkan ara yüzeyindeki basınç farkının ortalama eğrilikle orantılı olmasıdır. Açık bir sabun filmi için basınç farkı sıfırdır, dolayısıyla ortalama eğrilik sıfırdır ve minimal yüzeyler sıfır ortalama eğrilik özelliğine sahiptir.
İletişim açıları
Herhangi bir sıvının yüzeyi, o sıvı ile başka bir ortam arasındaki bir ara yüzeydir. Örneğin bir havuzun üst yüzeyi, havuz suyu ile hava arasında bir ara yüzeydir. O halde yüzey gerilimi tek başına sıvının bir özelliği değil, sıvının başka bir ortamla olan ara yüzeyinin bir özelliğidir. Eğer bir sıvı bir kabın içindeyse, üst yüzeyindeki sıvı/hava arayüzeyinin yanı sıra, sıvı ile kabın duvarları arasında da bir arayüzey vardır. Sıvı ile hava arasındaki yüzey gerilimi genellikle sıvının kabın duvarlarıyla olan yüzey geriliminden farklıdır (daha büyüktür). İki yüzeyin birleştiği yerde geometri tüm kuvvetleri dengeleyecektir.
İki yüzeyin birleştiği yerde, bir temas açısı oluştururlar, θ {\displaystyle \scriptstyle \theta } 


γ l a > γ l s - γ s a > 0 {\displaystyle \gamma _{\mathrm {la} }\ >\ \gamma _{\mathrm {ls} }-\gamma _{\mathrm {sa} }\ >\ 0}
Diyagramda, hem dikey hem de yatay kuvvetler, denge olarak bilinen temas noktasında tam olarak iptal edilmelidir. f l a {\displaystyle \scriptstyle f_{\mathrm {la} yatay bileşeni }}

f A = f l a sin θ {\displaystyle f_{\mathrm {A} }\ =\ f_{\mathrm {la} }\sin \theta }
Ancak daha önemli olan kuvvet dengesi dikey yöndedir. f l a {\displaystyle \scriptstyle f_{\mathrm {la}'nın dikey bileşeni }}

f l s - f s a = - f l a cos θ {\displaystyle f_{\mathrm {ls} }-f_{\mathrm {sa} }\ =\ -f_{\mathrm {la} }\cos \theta }
| Sıvı | Katı | Temas açısı | |||
| su |
| 0° | |||
| dietil eter | |||||
| karbon tetraklorür | |||||
| gliserol | |||||
| asetik asit | |||||
| su | parafin mumu | 107° | |||
| Gümüş | 90° | ||||
| metil iyodür | soda-kireç bardağı | 29° | |||
| kurşun cam | 30° | ||||
| erimiş kuvars | 33° | ||||
| soda-kireç bardağı | 140° | ||||
| Bazı sıvı-katı temas açıları | |||||
Kuvvetler kendi yüzey gerilimleriyle doğru orantılı olduğundan, ayrıca
γ l s - γ s a = - γ l a cos θ {\displaystyle \gamma _{\mathrm {ls} }-\gamma _{\mathrm {sa} }\ =\ -\gamma _{\mathrm {la} }\cos \theta }
nerede
· γ l s {\displaystyle \scriptstyle \gamma _{\mathrm {ls} }}
· γ l a {\displaystyle \scriptstyle \gamma _{\mathrm {la} }}
· γ s a {\displaystyle \scriptstyle \gamma _{\mathrm {sa} }}
· θ {\displaystyle \scriptstyle \theta }
Bu, sıvı-katı ve katı-hava yüzey gerilimi arasındaki fark, γ l s - γ s a {\displaystyle \scriptstyle \gamma _{\mathrm {ls} }-\gamma _{\mathrm {sa} }} 


Aynı ilişki sağdaki diyagramda da mevcuttur. Ancak bu durumda temas açısı 90°'den küçük olduğu için sıvı-katı/katı-hava yüzey gerilimi farkının negatif olması gerektiğini görüyoruz:
γ l a > 0 > γ l s - γ s a {\displaystyle \gamma _{\mathrm {la} }\ >\ 0\ >\ \gamma _{\mathrm {ls} }-\gamma _{\mathrm {sa} }}
Özel temas açıları
Temas açısının 90°'ye eşit olduğu su-gümüş arayüzeyinin özel durumunda, sıvı-katı/katı-hava yüzey gerilimi farkının tam olarak sıfır olduğunu gözlemleyin.
Bir diğer özel durum ise temas açısının tam olarak 180° olduğu durumdur. Özel olarak hazırlanmış teflonlu su buna yaklaşır. 180°'lik temas açısı, sıvı-katı yüzey gerilimi sıvı-hava yüzey gerilimine tam olarak eşit olduğunda meydana gelir.
γ l a = γ l s - γ s a > 0 θ = 180 ∘ {\displaystyle \gamma _{\mathrm {la} }\ =\ \gamma _{\mathrm {ls} }-\gamma _{\mathrm {sa} }\ >\ 0\qquad \theta \ =\ 180^{\circ }}
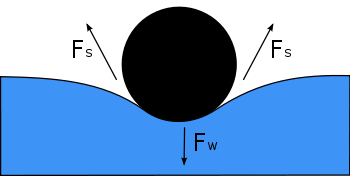
Diyagram, enine kesitte, su yüzeyinde yüzen bir iğneyi göstermektedir. Ağırlığı, Fw , yüzeye baskı yapar ve her iki taraftaki yüzey gerilim kuvvetleri, Fs , ile dengelenir ve her biri iğneye temas ettiği noktalarda su yüzeyine paraleldir. İki Fs okunun yatay bileşenlerinin zıt yönleri gösterdiğine, dolayısıyla birbirlerini iptal ettiklerine, ancak dikey bileşenlerin aynı yönü gösterdiğine ve dolayısıyla Fw 'yi dengelemek için toplandıklarına dikkat edin.
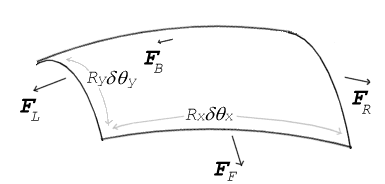
Küçük (diferansiyel) bir yüzey parçası üzerinde etkili olan yüzey gerilim kuvvetleri. δθx ve δθy yamanın boyutları üzerindeki bükülme miktarını gösterir. Gerilim kuvvetlerinin basınç ile dengelenmesi Young-Laplace denklemine yol açar

Minimal yüzey
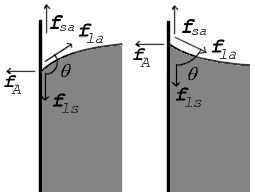
Temas noktasındaki kuvvetler 90°'den büyük (sol) ve 90°'den küçük (sağ) temas açıları için gösterilmiştir
Ölçüm yöntemleri
Yüzey gerilimi kendini çeşitli etkilerle gösterdiğinden, ölçümü için bir dizi yol sunar. Hangi yöntemin en uygun olduğu, ölçülen sıvının doğasına, geriliminin ölçüleceği koşullara ve deforme olduğunda yüzeyinin kararlılığına bağlıdır.
- Du Noüy Ring yöntemi: Yüzey veya arayüzey gerilimini ölçmek için kullanılan geleneksel yöntem. Yüzeyin veya arayüzeyin ıslanma özelliklerinin bu ölçüm tekniği üzerinde çok az etkisi vardır. Yüzey tarafından halka üzerine uygulanan maksimum çekme ölçülür.
- Du Noüy-Padday yöntemi: Du Noüy yönteminin küçültülmüş bir versiyonu, maksimum çekmeyi kaydetmek için yüksek hassasiyetli bir mikrobalans ile birlikte halka yerine küçük çaplı bir metal iğne kullanır. Bu yöntemin avantajı, çok küçük numune hacimlerinin (birkaç on mikrolitreye kadar), kaldırma kuvvetini düzeltmeye gerek kalmadan (uygun geometriye sahip bir iğne veya çubuk için) çok yüksek hassasiyetle ölçülebilmesidir. Ayrıca, ölçüm çok hızlı bir şekilde, minimum 20 saniye içinde gerçekleştirilebilir. İlk ticari çok kanallı tansiyometreler [CMCeeker] yakın zamanda bu prensibe dayalı olarak üretilmiştir.
- Wilhelmy plaka yöntemi: Özellikle uzun zaman aralıklarında yüzey gerilimini kontrol etmek için uygun evrensel bir yöntemdir. Çevresi bilinen dikey bir plaka bir teraziye bağlanır ve ıslanmadan kaynaklanan kuvvet ölçülür.
- Dönen damla yöntemi: Bu teknik, düşük arayüzey gerilimlerini ölçmek için idealdir. Ağır bir faz içindeki bir damlanın çapı, her ikisi de döndürülürken ölçülür.
- Kolye düşürme yöntemi: Yüzey ve arayüzey gerilimi, yüksek sıcaklık ve basınçlarda bile bu teknikle ölçülebilir. Bir damlanın geometrisi optik olarak analiz edilir. Ayrıntılar için Damla bölümüne bakınız.
- Kabarcık basıncı yöntemi (Jaeger yöntemi): Kısa yüzey yaşlarında yüzey gerilimini belirlemeye yönelik bir ölçüm tekniği. Her bir kabarcığın maksimum basıncı ölçülür.
- Damla hacmi yöntemi: Arayüzey yaşının bir fonksiyonu olarak arayüzey gerilimini belirlemeye yönelik bir yöntem. Bir yoğunluktaki sıvı, farklı yoğunluktaki ikinci bir sıvıya pompalanır ve üretilen damlalar arasındaki süre ölçülür.
- Kılcal yükselme yöntemi: Bir kılcal damarın ucu çözeltinin içine daldırılır. Çözeltinin kapiler içinde ulaştığı yükseklik, aşağıda tartışılan denklem ile yüzey gerilimi ile ilişkilidir.
- Stalagmometrik yöntem: Bir damla sıvıyı tartma ve okuma yöntemi.
- Sapsız damla yöntemi: Bir substrat üzerine bir damla yerleştirerek ve temas açısını ölçerek yüzey gerilimini ve yoğunluğunu belirlemeye yönelik bir yöntem (bkz. Sessiz damla tekniği).
- Havaya kaldırılan damlaların titreşim frekansı: Süper akışkanın yüzey gerilimi4 He, manyetikler tarafından havada tutulan damlaların titreşim salınımlarının doğal frekansı incelenerek ölçülmüştür. Bu değerin T = 0° K'de 0,375 dyn/cm olduğu tahmin edilmektedir.

Yüzey gerilimi, bir gonyometre üzerinde asılı damla yöntemi kullanılarak ölçülebilir.
Etkileri
Dikey bir tüp içindeki sıvı
Eski tip bir cıvalı barometre, kısmen cıva ile doldurulmuş ve doldurulmamış hacimde bir vakum (Torricelli'nin vakumu olarak adlandırılır) bulunan yaklaşık 1 cm çapında dikey bir cam tüpten oluşur (sağdaki şemaya bakın). Tüpün ortasındaki cıva seviyesinin kenarlardan daha yüksek olduğuna ve cıvanın üst yüzeyini kubbe şekline getirdiğine dikkat edin. Cıvanın üst yüzeyi tüpün tüm kesiti boyunca düz olsaydı, tüm cıva sütununun kütle merkezi biraz daha alçak olurdu. Ancak kubbe şeklindeki üst yüzey, tüm cıva kütlesine biraz daha az yüzey alanı sağlar. Yine bu iki etki birleşerek toplam potansiyel enerjiyi en aza indirir. Böyle bir yüzey şekli dışbükey menisküs olarak bilinir.
Yüzeyin camla temas eden kısmı da dahil olmak üzere tüm cıva kütlesinin yüzey alanını dikkate alıyoruz, çünkü cıva cama hiç yapışmaz. Dolayısıyla cıvanın yüzey gerilimi, camla temas ettiği yer de dahil olmak üzere tüm yüzey alanına etki eder. Eğer tüp cam yerine bakırdan yapılmış olsaydı, durum çok farklı olurdu. Cıva bakıra agresif bir şekilde yapışır. Dolayısıyla bakır bir tüpte, tüpün merkezindeki cıva seviyesi kenarlardan daha düşük olacaktır (yani içbükey bir menisküs olacaktır). Sıvının kabının duvarlarına yapıştığı bir durumda, sıvının yüzey alanının kapla temas eden kısmının negatif yüzey gerilimine sahip olduğunu düşünürüz. Sıvı daha sonra temas yüzey alanını maksimize etmek için çalışır. Dolayısıyla bu durumda kapla temas eden alanın artırılması potansiyel enerjiyi artırmak yerine azaltır. Bu azalma, sıvının kabın duvarları yakınında kaldırılmasıyla ilişkili artan potansiyel enerjiyi telafi etmek için yeterlidir.
Bir tüp yeterince darsa ve sıvının duvarlara yapışması yeterince güçlüyse, yüzey gerilimi, kılcal hareket olarak bilinen bir olguyla sıvıyı tüpten yukarı çekebilir. Kolonun yükseldiği yükseklik şu şekilde verilir:
h = 2 γ l a cos θ ρ g r {\displaystyle h\ =\ {\frac {2\gamma _{\mathrm {la} }\cos \theta }{\rho gr}}
nerede
· h {\displaystyle \scriptstyle h}
· γ l a {\displaystyle \scriptstyle \gamma _{\mathrm {la} }}
· ρ {\displaystyle \scriptstyle \rho }
· r {\displaystyle \scriptstyle r}
· g {\displaystyle \scriptstyle g}
· θ {\displaystyle \scriptstyle \theta }

Bir yüzey üzerinde su birikintileri
Yatay düz bir cam levha üzerine cıva dökülmesi, algılanabilir kalınlıkta bir su birikintisine neden olur. Su birikintisi sadece yarım santimetreden biraz daha kalın olduğu noktaya kadar yayılır ve daha ince olmaz. Bu da yine cıvanın güçlü yüzey geriliminin etkisinden kaynaklanmaktadır. Sıvı kütlesi düzleşir, çünkü bu cıvanın mümkün olduğunca büyük bir kısmını mümkün olduğunca düşük bir seviyeye getirir, ancak yüzey gerilimi aynı zamanda toplam yüzey alanını azaltmak için hareket eder. Sonuç, neredeyse sabit kalınlıkta bir su birikintisinin uzlaşmasıdır.
Aynı yüzey gerilimi gösterimi su, kireçli su ve hatta tuzlu su ile de yapılabilir, ancak sadece sıvı düz yüzey malzemesine yapışmıyorsa. Balmumu böyle bir maddedir. Pürüzsüz, düz, yatay bir balmumu yüzeyine, örneğin mumlu bir cam tabakaya dökülen su, cama dökülen cıva ile benzer şekilde davranacaktır.
Temas açısı 180° olan bir yüzey üzerindeki sıvı birikintisinin kalınlığı şu şekilde verilir:
h = 2 γ g ρ {\displaystyle h\ =\ 2{\sqrt {\frac {\gamma }{g\rho }}}}
nerede
| h {\displaystyle \scriptstyle h} |
| γ {\displaystyle \scriptstyle \gamma } |
| g {\displaystyle \scriptstyle g} |
| ρ {\displaystyle \scriptstyle \rho } |
Gerçekte, su birikintilerinin kalınlıkları yukarıdaki formülle tahmin edilenden biraz daha az olacaktır çünkü çok az yüzey herhangi bir sıvıyla 180°'lik bir temas açısına sahiptir. Temas açısı 180°'den az olduğunda, kalınlık şu şekilde verilir:
h = 2 γ l a ( 1 - cos θ ) g ρ . {\displaystyle h\ =\ {\sqrt {\frac {2\gamma _{\mathrm {la} }\left(1-\cos \theta \right)}{g\rho }}}. }
Cam üzerindeki cıva için, γHg = 487 dyn/cm, ρHg = 13,5 g/cm3 ve θ = 140°, bu da hHg = 0,36 cm verir. 25°C'de parafin üzerindeki su için, γ = 72 dyn/cm, ρ = 1.0 g/cm3 ve θ = 107°, bu da hH2O = 0.44 cm verir.
Formül ayrıca temas açısı 0° olduğunda sıvının yüzey üzerinde mikro-ince bir tabaka halinde yayılacağını öngörmektedir. Böyle bir yüzeyin sıvı tarafından tamamen ıslatılabilir olduğu söylenir.
Akarsuların damlalara ayrılması
Günlük hayatta hepimiz, musluktan çıkan bir su akışının, akış musluktan ne kadar düzgün bir şekilde yayılırsa yayılsın, damlacıklara ayrılacağını gözlemleriz. Bunun nedeni, tamamen yüzey geriliminin etkilerinin bir sonucu olan Plateau-Rayleigh kararsızlığı adı verilen bir olgudur.
Bu istikrarsızlığın açıklaması, akıştaki küçük pertürbasyonların varlığıyla başlar. Akış ne kadar düzgün olursa olsun bunlar her zaman mevcuttur. Pertürbasyonlar sinüzoidal bileşenlere ayrılırsa, bazı bileşenlerin zamanla büyüdüğünü, diğerlerinin ise zamanla azaldığını görürüz. Zamanla büyüyenler arasında bazıları diğerlerinden daha hızlı büyür. Bir bileşenin azalması ya da büyümesi ve ne kadar hızlı büyüdüğü tamamen dalga sayısının (santimetre başına kaç tepe ve çukur düştüğünün bir ölçüsü) ve orijinal silindirik akışın yarıçapının bir fonksiyonudur.
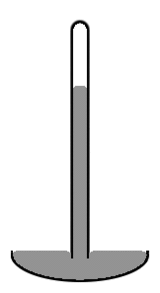
Cıvalı barometre diyagramı
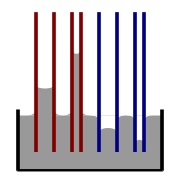
Kılcal damar yükselme ve alçalmasının gösterimi. Kırmızı = 90°'den küçük temas açısı; mavi = 90°'den büyük temas açısı
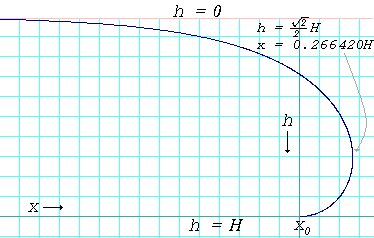
Temas açısının 180° olduğu bir su birikintisinin kenarının profil eğrisi. Eğri formül tarafından verilir: x - x 0 = 1 2 H cosh - 1 ( H h ) - H 1 - h 2 H 2 {\displaystyle \scriptstyle x-x_{0}\ =\ {\frac {1}{2}}H\cosh ^{-1}\left({\frac {H}{h}}\right)-H{\sqrt {1-{\frac {h^{2}}{H^{2}}}}}}

Pürüzsüz ve temiz bir yüzey üzerindeki küçük su birikintileri hissedilebilir kalınlığa sahiptir.
Düşük temas açısının su birikintisi derinliğinin azalmasına nasıl yol açtığının gösterimi
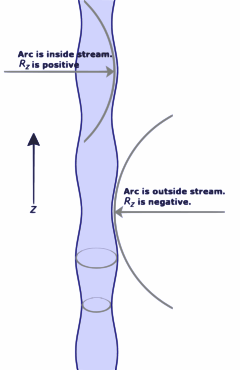
Damlalar halinde kırılan bir jetin ara aşaması. Eksenel yöndeki eğrilik yarıçapları gösterilmiştir. Akışın yarıçapı için denklem R ( z ) = R 0 + A k cos ( k z ) {\displaystyle \scriptstyle R\left(z\right)=R_{0}+A_{k}\cos \left(kz\right)}




Veri tablosu
| Çeşitli sıvıların havaya karşı dyn/cm cinsinden yüzey gerilimiKarışım | ||
| Sıvı | Sıcaklık °C | Yüzey gerilimi, γ |
| Asetik asit | 20 | 27.6 |
| Asetik asit (%40,1) + Su | 30 | 40.68 |
| Asetik asit (%10.0) + Su | 30 | 54.56 |
| Aseton | 20 | 23.7 |
| Dietil eter | 20 | 17.0 |
| Etanol | 20 | 22.27 |
| Etanol (%40) + Su | 25 | 29.63 |
| Etanol (%11,1) + Su | 25 | 46.03 |
| Gliserol | 20 | 63 |
| n-Hekzan | 20 | 18.4 |
| Hidroklorik asit 17.7M sulu çözelti | 20 | 65.95 |
| İzopropanol | 20 | 21.7 |
| Sıvı Azot | -196 | 8.85 |
| 15 | 487 | |
| Metanol | 20 | 22.6 |
| n-Oktan | 20 | 21.8 |
| Sodyum klorür 6.0M sulu çözelti | 20 | 82.55 |
| Sükroz (%55) + su | 20 | 76.45 |
| Su | 0 | 75.64 |
| Su | 25 | 71.97 |
| Su | 50 | 67.91 |
| Su | 100 | 58.85 |
Efektler Galerisi
· 
Bir kaşıktan sıçrayan hareketli bir su tabakasının parçalanması.
· 
Bir ele yapışan akan suyun fotoğrafı. Yüzey gerilimi, akış ile el arasında su tabakası oluşturur.
· 
Bir sabun köpüğü yüzey gerilim kuvvetlerini iç pnömatik basınca karşı dengeler.
· 
Yüzey gerilimi bir madeni paranın batmasını engeller: madeni para tartışmasız bir şekilde sudan daha yoğundur, bu nedenle kaldırma kuvvetinin kütleyi dengelemesi için kendi hacminden daha büyük bir hacmi yer değiştirmesi gerekir.
· 
Bir papatya. Çiçeğin tamamı (bozulmamış) serbest yüzey seviyesinin altındadır. Su, kenarı etrafında düzgün bir şekilde yükselir. Yüzey gerilimi, suyun taç yapraklar arasındaki havayı doldurmasını ve muhtemelen çiçeğe batmasını önler.
· 
Metal bir ataş su üzerinde yüzer. Genellikle su taşması olmadan birkaç tane dikkatlice eklenebilir.
· .jpg)
Bir alüminyum para 10 °C'de suyun yüzeyinde yüzmektedir. Herhangi bir ekstra ağırlık madeni parayı dibe indirecektir.
Sorular ve Yanıtlar
S: Yüzey gerilimi nedir?
C: Yüzey gerilimi, bir sıvının yüzeyinin güçlü olduğu ve bir ağırlığı tutabildiği bir etkidir. Bazı küçük şeylerin normalde yüzemeyecekleri halde yüzeyde yüzebilmelerine neden olur ve bazı böceklerin (örneğin su striderleri) su yüzeyinde koşmasına izin verir.
S: Yüzey gerilimine ne sebep olur?
C: Yüzey gerilimi sıvı içindeki moleküllerin birbirini çekmesinden (kohezyon) kaynaklanır.
S: Yüzey geriliminin boyutları nelerdir?
C: Yüzey gerilimi birim uzunluk başına kuvvet veya birim alan başına enerji boyutuna sahiptir. Bu ikisi eşdeğerdir ancak birim alan başına enerjiden bahsederken insanlar yüzey enerjisi terimini kullanırlar ki bu sadece sıvılar için değil katılar için de geçerli olması anlamında daha genel bir terimdir.
S: Yüzey gerilimi malzeme bilimini nasıl etkiler?
C: Malzeme biliminde yüzey gerilimi, yüzey gerilimi ya da yüzey serbest enerjisi için kullanılır.
S: Kohezyon yüzey gerilimine nasıl katkıda bulunur?
C: Kohezyon, bir sıvıdaki moleküllerin birbirine çekilmesine neden olarak yüzey gerilimine katkıda bulunur, bu da yüzeylerinde ağırlığı taşıyabilen ve belirli nesnelerin veya canlıların (örneğin, su striderleri) onunla başka türlü yapabileceklerinden farklı bir şekilde etkileşime girmesine izin veren güçlü bir bağ oluşturur.
S: Bu özelliğin sıvıların diğer özelliklerinden farkı nedir?
C: Bu özellik sıvıların diğer özelliklerinden farklıdır, çünkü nesnelerin onlarla içlerinde veya bir bütün olarak toplu davranışlarından ziyade yüzeylerinde nasıl etkileşime girdiklerini etkiler.
Ansiklopedi içinde ara