Logaritmik ölçek
Logaritmik ölçek, büyük bir miktar aralığı olduğunda kullanılan bir ölçektir. Yaygın kullanım alanları arasında deprem şiddeti, ses yüksekliği, ışık yoğunluğu ve çözeltilerin pH'ı yer alır.
Standart bir doğrusal ölçek yerine büyüklük derecelerine dayanır. Ölçekteki her bir işaretin değeri, bir önceki işaretteki değerin bir sabit ile çarpımıdır.
Logaritmik ölçekler, ölçeklerdeki uzunlukları toplayarak veya çıkararak sayıları çarpmak veya bölmek için sürgülü cetvellerde de kullanılır.
Logaritmik ölçek, veriler geniş bir değer aralığını kapsadığında yararlı olabilir - logaritma bunu daha yönetilebilir bir aralığa indirir.
Bazı duyularımız logaritmik bir şekilde çalışır (gerçek giriş gücünün çarpılması algılanan sinyal gücüne bir sabit ekler, bkz: Stevens'ın güç yasası). Bu da bu girdi miktarları için logaritmik ölçekleri özellikle uygun hale getirir. Özellikle işitme duyumuz, frekansların eşit katlarını perdede eşit farklılıklar olarak algılar.
Çoğu logaritmik ölçekte, temel niceliğin küçük katları (veya oranları) logaritmik ölçünün küçük (muhtemelen negatif) değerlerine karşılık gelir.
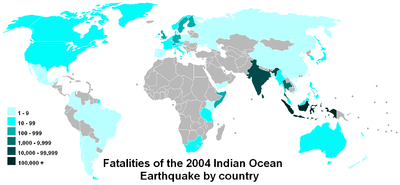
Log ölçeği, bu haritada olduğu gibi geniş bir aralığı kapsayan değerleri karşılaştırmayı kolaylaştırır
Sürgülü cetvelin iki logaritmik ölçeği
Örnekler
Bu tür ölçeklerin iyi bilinen örnekleri şunlardır:
- Depremlerin gücü ve yeryüzündeki hareket için Richter büyüklük ölçeği ve moment büyüklük ölçeği (MMS).
- bel ve akustik güç (ses yüksekliği) ve elektrik gücü için desibel ve neper;
- fotoğrafik pozlama oranları için f-stop sayma;
- Düşük olasılıkları, gerçekleşmeme olasılıklarının ondalık açılımındaki 'dokuz' sayısına göre derecelendirin: örneğin, 10−5 olasılıkla başarısız olacak bir sistem %99,999 güvenilirdir: "beş dokuz".
- Termodinamikte entropi.
- Bilgi teorisinde bilgi.
- Toprağın parçacık boyutu dağılım eğrileri
Bazı logaritmik ölçekler, temel niceliğin büyük değerlerinin (veya oranlarının) logaritmik ölçünün küçük değerlerine karşılık geleceği şekilde tasarlanmıştır. Bu tür ölçeklere örnek olarak şunlar verilebilir:
- Asitlik için pH;
- yıldızların parlaklığı için yıldız büyüklüğü ölçeği;
Logaritmik ölçek aynı zamanda bir grafiğin bir veya her iki tarafına 1 rakamıyla işaretlenmiş noktadan c-log(x) uzaklığında bir x rakamının basıldığı grafiksel bir ölçektir. Bir sürgülü cetvel logaritmik ölçeklere sahiptir ve nomogramlar genellikle logaritmik ölçekler kullanır. Logaritmik bir ölçekte, büyüklük sırasındaki eşit bir fark, eşit bir mesafe ile temsil edilir. İki sayının geometrik ortalaması sayıların ortasıdır.
Logaritmik grafik kağıdı, bilgisayar grafikleri ortaya çıkmadan önce temel bir bilimsel araçtı. Bir log ölçeğine sahip kağıt üzerindeki grafikler, üstel yasaları ve log-log kağıt üzerindeki güç yasalarını düz çizgiler olarak gösterebilir (bkz. semilog grafik, log-log grafik).
Sorular ve Yanıtlar
S: Logaritmik ölçek nedir?
C: Logaritmik ölçek, büyük bir miktar aralığı olduğunda kullanılan bir ölçektir.
S: Logaritmik ölçekte ölçülebilen bazı şeylere örnekler nelerdir?
C: Depremin şiddeti, ses yüksekliği, ışık yoğunluğu, salgın hastalıkların yayılma oranları ve çözeltilerin pH'ı logaritmik ölçekte ölçülebilir.
S: Logaritmik ölçeğin standart doğrusal ölçekten farkı nedir?
C: Logaritmik ölçek, standart bir doğrusal ölçek yerine büyüklük mertebelerine dayanır. Ölçekteki her bir işaretin değeri, bir önceki işaretteki değerin bir sabit ile çarpımıdır.
S: Logaritmik ölçek kullanmanın faydası nedir?
C: Logaritmik ölçek, geniş bir değer aralığını daha yönetilebilir bir aralığa indirgeyebilir, bu da geniş bir değer aralığını kapsayan verilerle uğraşırken yardımcı olabilir.
S: Stevens'ın güç yasası nedir ve logaritmik ölçeklerle nasıl ilişkilidir?
C: Stevens'ın güç yasası, bazı duyularımızın logaritmik bir şekilde nasıl çalıştığını açıklar; burada gerçek giriş gücünün çarpılması, algılanan sinyal gücüne bir sabit ekler. Bu durum, bu girdi miktarları için logaritmik ölçekleri özellikle uygun kılmaktadır.
S: Logaritmik ölçek ses yüksekliğini ölçmek için neden özellikle kullanışlıdır?
C: İşitme duyumuz frekansların eşit katlarını perdede eşit farklılıklar olarak algılar, bu nedenle logaritmik bir ölçek ses frekansı ve algılanan ses yüksekliği arasındaki bu ilişkiyi doğru bir şekilde temsil edebilir.
S: Temel niceliğin küçük katları ile çoğu logaritmik ölçekteki logaritmik ölçü arasındaki ilişki nedir?
C: Çoğu logaritmik ölçekte, temel niceliğin küçük katları (veya oranları) logaritmik ölçünün küçük (muhtemelen negatif) değerlerine karşılık gelir.
Ansiklopedi içinde ara