Harmonik seriler (matematik)

Matematikte harmonik seri, ıraksak sonsuz seridir:

∑ n = 1 ∞ 1 n = 1 + 1 2 + 1 3 + 1 4 + 1 5 + ⋯ {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots } {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots }

Iraksak, daha fazla terim ekledikçe toplamın büyümesinin asla durmayacağı anlamına gelir. Tek bir sonlu değere doğru gitmez.

Sonsuz, her zaman başka bir terim ekleyebileceğiniz anlamına gelir. Serinin son terimi yoktur.

Adı müzikteki harmonik fikrinden gelir: titreşen bir telin üst tonlarının dalga boyları, telin temel dalga boyunun 1/2, 1/3, 1/4, vb. İlk terim dışında, serinin her terimi, iki yanındaki terimlerin harmonik ortalamasıdır. Harmonik ortalama ifadesi de müzikten gelmektedir.

Tarih

Harmonik serilerin ıraksadığı gerçeği ilk olarak 14. yüzyılda Nicole Oresme tarafından kanıtlanmış, ancak unutulmuştur. Kanıtlar 17. yüzyılda Pietro Mengoli, Johann Bernoulli ve Jacob Bernoulli tarafından verilmiştir.

Harmonik diziler mimarlar tarafından kullanılmıştır. Barok dönemde mimarlar bunları kat planlarının oranlarında, yüksekliklerde ve kilise ve sarayların mimari detayları arasındaki ilişkilerde kullanmışlardır.

Ayrışma

Harmonik serilerin ıraksamasına ilişkin iyi bilinen birkaç kanıt vardır. Bunlardan birkaçı aşağıda verilmiştir.

Karşılaştırma testi

Iraksaklığı kanıtlamanın bir yolu, harmonik seriyi, her bir paydanın ikinin bir sonraki en büyük kuvvetiyle değiştirildiği başka bir ıraksak seriyle karşılaştırmaktır:

1 + 1 2 + 1 3 + 1 4 + 1 5 + 1 6 + 1 7 + 1 8 + 1 9 + ⋯ ≥ 1 + 1 2 + 1 4 + 1 4 + 1 8 + 1 8 + 1 8 + 1 16 + ⋯ {\displaystyle {\begin{aligned}&{}1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+{\frac {1}{6}}+{\frac {1}{7}}+{\frac {1}{8}}+{\frac {1}{9}}+\cdots \\[12pt]\geq {}&1+{\frac {1}{2}}+{\frac {1}{\color {red}{\mathbf {4} }}}+{\frac {1}{4}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{8}}+{\frac {1}{\color {red}{\mathbf {16} }}}+\cdots \end{aligned}} {\displaystyle {\begin{aligned}&{}1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+{\frac {1}{6}}+{\frac {1}{7}}+{\frac {1}{8}}+{\frac {1}{9}}+\cdots \\[12pt]\geq {}&1+{\frac {1}{2}}+{\frac {1}{\color {red}{\mathbf {4} }}}+{\frac {1}{4}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{8}}+{\frac {1}{\color {red}{\mathbf {16} }}}+\cdots \end{aligned}}}

Harmonik serinin her bir terimi ikinci serinin karşılık gelen teriminden büyük veya ona eşittir ve bu nedenle harmonik serinin toplamı ikinci serinin toplamından büyük veya ona eşit olmalıdır. Ancak, ikinci serinin toplamı sonsuzdur:

1 + ( 1 2 ) + ( 1 4 + 1 4 ) + ( 1 8 + 1 8 + 1 8 + 1 8 ) + ( 1 16 + ⋯ + 1 16 ) + ⋯ = 1 + 1 2 + 1 2 + 1 2 + 1 2 + ⋯ = ∞ {\displaystyle {\begin{aligned}&{}1+\left({\frac {1}{2}}\right)+\left({\frac {1}{4}}\!+\!{\frac {1}{4}}\right)+\left({\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\right)+\left({\frac {1}{16}}\!+\!\cdots \!+\!{\frac {1}{16}}\right)+\cdots \\[12pt]={}&1+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+\cdots =\infty \end{aligned}} {\displaystyle {\begin{aligned}&{}1+\left({\frac {1}{2}}\right)+\left({\frac {1}{4}}\!+\!{\frac {1}{4}}\right)+\left({\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\right)+\left({\frac {1}{16}}\!+\!\cdots \!+\!{\frac {1}{16}}\right)+\cdots \\[12pt]={}&1+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+\cdots =\infty \end{aligned}}}

Buradan (karşılaştırma testiyle) harmonik serilerin toplamının da sonsuz olması gerektiği sonucu çıkar. Daha doğrusu, yukarıdaki karşılaştırma şunu kanıtlar

∑ n = 1 2 k 1 n ≥ 1 + k 2 {\displaystyle \sum _{n=1}^{2^{k}}{\frac {1}{n}}\geq 1+{\frac {k}{2}}} {\displaystyle \sum _{n=1}^{2^{k}}{\frac {1}{n}}\geq 1+{\frac {k}{2}}}

her pozitif k tamsayısı için.

Nicole Oresme tarafından yaklaşık 1350 yılında önerilen bu ispat, ortaçağ matematiğinin en yüksek noktası olarak kabul edilir. Bugün hala matematik derslerinde öğretilen standart bir ispattır.

İntegral testi

Harmonik serinin ıraksadığını, toplamını uygun olmayan bir integral ile karşılaştırarak kanıtlamak mümkündür. Sağdaki şekilde gösterilen dikdörtgenlerin düzenini düşünün. Her bir dikdörtgen 1 birim genişliğinde ve 1/n birim yüksekliğindedir, dolayısıyla sonsuz sayıda dikdörtgenin toplam alanı harmonik serilerin toplamıdır:

dikdörtgenlerin alanı = 1 + 1 2 + 1 3 + 1 4 + 1 5 + ⋯ {\displaystyle {\begin{array}{c}{\text{area of}}\{\text{rectangles}}\end{array}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots } {\displaystyle {\begin{array}{c}{\text{area of}}\\{\text{rectangles}}\end{array}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots }

1'den sonsuza kadar y = 1/x eğrisinin altındaki toplam alan, ıraksak bir yanlış integral ile verilir:

eğri altında kalan alan = ∫ 1 ∞ 1 x d x = ∞ . {\displaystyle {\begin{array}{c}{\text{area under}}\{\text{curve}}\end{array}}=\int _{1}^{\infty }{\frac {1}{x}}\,dx=\infty . } {\displaystyle {\begin{array}{c}{\text{area under}}\\{\text{curve}}\end{array}}=\int _{1}^{\infty }{\frac {1}{x}}\,dx=\infty .}

Bu alan tamamen dikdörtgenlerin içinde yer aldığından, dikdörtgenlerin toplam alanı da sonsuz olmalıdır. Bu da şunu kanıtlar

∑ n = 1 k 1 n > ∫ 1 k + 1 1 x d x = ln ( k + 1 ) . {\displaystyle \sum _{n=1}^{k}{\frac {1}{n}}>\int _{1}^{k+1}{\frac {1}{x}}\,dx=\ln(k+1). } {\displaystyle \sum _{n=1}^{k}{\frac {1}{n}}>\int _{1}^{k+1}{\frac {1}{x}}\,dx=\ln(k+1).}

Bu argümanın genelleştirilmesi integral testi olarak bilinir.

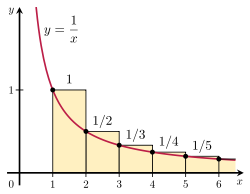
İntegral testinin gösterimi.Zoom
İntegral testinin gösterimi.

Farklılaşma oranı

Harmonik seri çok yavaş ayrışır. Örneğin, ilk 1043 terimin toplamı 100'den azdır. Bunun nedeni serinin kısmi toplamlarının logaritmik büyümeye sahip olmasıdır. Özellikle,

∑ n = 1 k 1 n = ln k + γ + ε k ≤ ( ln k ) + 1 {\displaystyle \sum _{n=1}^{k}{\frac {1}{n}}=\ln k+\gamma +\varepsilon _{k}\leq (\ln k)+1} {\displaystyle \sum _{n=1}^{k}{\frac {1}{n}}=\ln k+\gamma +\varepsilon _{k}\leq (\ln k)+1}

Burada γ Euler-Mascheroni sabitidir ve εk ~ 1/2k olup k sonsuza giderken 0'a yaklaşır. Leonhard Euler hem bunu hem de sadece asal sayıların terslerini içeren toplamın da ıraksadığını kanıtlamıştır:

∑ p asal 1 p = 1 2 + 1 3 + 1 5 + 1 7 + 1 11 + 1 13 + 1 17 + ⋯ = ∞ . {\displaystyle \sum _{p{\text{ prime }}}{\frac {1}{p}}={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+{\frac {1}{11}}+{\frac {1}{13}}+{\frac {1}{17}}+\cdots =\infty . } {\displaystyle \sum _{p{\text{ prime }}}{\frac {1}{p}}={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+{\frac {1}{11}}+{\frac {1}{13}}+{\frac {1}{17}}+\cdots =\infty .}

Kısmi toplamlar

İlk otuz harmonik sayı

n

Harmonik serilerin kısmi toplamı, H n

 

kesir olarak ifade edilir

ondalık

göreli büyüklük

 

1

1

~1

1

 

 

2

3

/2

~1.5

1.5

 

 

3

11

/6

~1.83333

1.83333

 

 

4

25

/12

~2.08333

2.08333

 

 

5

137

/60

~2.28333

2.28333

 

 

6

49

/20

~2.45

2.45

 

 

7

363

/140

~2.59286

2.59286

 

 

8

761

/280

~2.71786

2.71786

 

 

9

7129

/2520

~2.82897

2.82897

 

 

10

7381

/2520

~2.92897

2.92897

 

 

11

83711

/27720

~3.01988

3.01988

 

 

12

86021

/27720

~3.10321

3.10321

 

 

13

1145993

/360360

~3.18013

3.18013

 

 

14

1171733

/360360

~3.25156

3.25156

 

 

15

1195757

/360360

~3.31823

3.31823

 

 

16

2436559

/720720

~3.38073

3.38073

 

 

17

42142223

/12252240

~3.43955

3.43955

 

 

18

14274301

/4084080

~3.49511

3.49511

 

 

19

275295799

/77597520

~3.54774

3.54774

 

 

20

55835135

/15519504

~3.59774

3.59774

 

 

21

18858053

/5173168

~3.64536

3.64536

 

 

22

19093197

/5173168

~3.69081

3.69081

 

 

23

444316699

/118982864

~3.73429

3.73429

 

 

24

1347822955

/356948592

~3.77596

3.77596

 

 

25

34052522467

/8923714800

~3.81596

3.81596

 

 

26

34395742267

/8923714800

~3.85442

3.85442

 

 

27

312536252003

/80313433200

~3.89146

3.89146

 

 

28

315404588903

/80313433200

~3.92717

3.92717

 

 

29

9227046511387

/2329089562800

~3.96165

3.96165

 

 

30

9304682830147

/2329089562800

~3.99499

3.99499

 

 

Uzaklaşan harmonik serilerin sonlu kısmi toplamları,

H n = ∑ k = 1 n 1 k , {\displaystyle H_{n}=\sum _{k=1}^{n}{\frac {1}{k}},} {\displaystyle H_{n}=\sum _{k=1}^{n}{\frac {1}{k}},}

harmonik sayılar olarak adlandırılır.

Hn ve ln n arasındaki fark Euler-Mascheroni sabitine yakınsar. Herhangi iki harmonik sayı arasındaki fark asla bir tam sayı değildir. H1 = 1 dışında hiçbir harmonik sayı tam sayı değildir.

İlgili seriler

Alternatif harmonik seriler

Seri

∑ n = 1 ∞ ( - 1 ) n + 1 n = 1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ {\displaystyle \sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots } {\displaystyle \sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots }

alternatif harmonik seri olarak bilinir. Bu seri, alternatif seri testi ile yakınsar. Özellikle, toplam 2'nin doğal logaritmasına eşittir:

1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ = ln 2. {\displaystyle 1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots =\ln 2.} {\displaystyle 1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots =\ln 2.}

Alternatif harmonik seri, koşullu olarak yakınsak olsa da, kesinlikle yakınsak değildir: serideki terimler sistematik olarak yeniden düzenlenirse, genel olarak toplam farklı ve yeniden düzenlemeye bağlı olarak muhtemelen sonsuz olur.

Değişken harmonik seri formülü, doğal logaritma için Taylor serisi olan Mercator serisinin özel bir durumudur.

Arctangent için Taylor serisinden ilgili bir seri türetilebilir:

∑ n = 0 ∞ ( - 1 ) n 2 n + 1 = 1 - 1 3 + 1 5 - 1 7 + ⋯ = π 4 . {\displaystyle \sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}=1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+\cdots ={\frac {\pi }{4}}. } {\displaystyle \sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}=1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+\cdots ={\frac {\pi }{4}}.}

Bu, Leibniz serisi olarak bilinir.

Genel harmonik seriler

Genel harmonik seri şu şekildedir

∑ n = 0 ∞ 1 a n + b , {\displaystyle \sum _{n=0}^{\infty }{\frac {1}{an+b}},} {\displaystyle \sum _{n=0}^{\infty }{\frac {1}{an+b}},}

Burada a ≠ 0 ve b reel sayılardır ve b/a sıfır veya negatif bir tamsayı değildir.

Harmonik serilerle limit karşılaştırma testine göre, tüm genel harmonik seriler de sapmaktadır.

p-serisi

Harmonik serinin bir genellemesi, aşağıdaki gibi tanımlanan p-serisidir (veya hiperharmonik seridir)

∑ n = 1 ∞ 1 n p {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{p}}}} {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{p}}}}

Herhangi bir p reel sayısı için. p = 1 olduğunda, p serisi ıraksayan harmonik seridir. Ya integral testi ya da Cauchy yoğunlaşma testi, p serisinin tüm p > 1 için yakınsadığını (bu durumda aşırı harmonik seri olarak adlandırılır) ve tüm p ≤ 1 için ıraksadığını gösterir. Eğer p > 1 ise, p-serisinin toplamı ζ(p), yani p'de değerlendirilen Riemann zeta fonksiyonudur.

p = 2 için toplamı bulma problemine Basel problemi denir; Leonhard Euler bunun π2 /6 olduğunu göstermiştir. p = 3 için toplamın değeri Apéry sabiti olarak adlandırılır, çünkü Roger Apéry bunun irrasyonel bir sayı olduğunu kanıtlamıştır.

ln-serisi

P-serisi ile ilişkili olan ln-serisi şu şekilde tanımlanır

∑ n = 2 ∞ 1 n ( ln n ) p {\displaystyle \sum _{n=2}^{\infty }{\frac {1}{n(\ln n)^{p}}}} {\displaystyle \sum _{n=2}^{\infty }{\frac {1}{n(\ln n)^{p}}}}

Bunun p ≤ 1 için sapma gösterdiği ancak tüm p > 1 için yakınsadığı integral testi ile gösterilebilir.

φ-serisi

Herhangi bir dışbükey, gerçek değerli φ fonksiyonu için

lim sup u → 0 + φ ( u 2 ) φ ( u ) < 1 2 , {\displaystyle \limsup _{u\to 0^{+}{\frac {\varphi \left({\frac {u}{2}}\right)}{\varphi (u)}}<{\frac {1}{2}},} {\displaystyle \limsup _{u\to 0^{+}}{\frac {\varphi \left({\frac {u}{2}}\right)}{\varphi (u)}}<{\frac {1}{2}},}

seri

∑ n = 1 ∞ φ ( 1 n ) {\displaystyle \sum _{n=1}^{\infty }\varphi \left({\frac {1}{n}}\right)} {\displaystyle \sum _{n=1}^{\infty }\varphi \left({\frac {1}{n}}\right)}

yakınsaktır. []

Rastgele harmonik seriler

Rastgele harmonik seriler

∑ n = 1 ∞ s n n , {\displaystyle \sum _{n=1}^{\infty }{\frac {s_{n}}{n}},} {\displaystyle \sum _{n=1}^{\infty }{\frac {s_{n}}{n}},}

Burada sn +1 ve -1 değerlerini 1/2 eşit olasılıkla alan bağımsız, özdeş dağılımlı rastgele değişkenlerdir, olasılık teorisinde 1 olasılıkla yakınsayan bir rastgele değişkenler serisi için iyi bilinen bir örnektir. Bu yakınsama gerçeği, Kolmogorov üç seri teoreminin ya da yakından ilişkili Kolmogorov maksimal eşitsizliğinin kolay bir sonucudur. Alberta Üniversitesi'nden Byron Schmuland, rastgele harmonik serinin özelliklerini daha fazla incelemiş ve yakınsak serinin bazı ilginç özelliklere sahip bir rastgele değişken olduğunu göstermiştir. Özellikle, +2 veya -2'de değerlendirilen bu rastgele değişkenin olasılık yoğunluk fonksiyonu 0.124999999999999999999999999999999999764... değerini alır ve 1/8'den 10'dan daha az farklılık gösterir−42 . Schmuland'ın makalesi, bu olasılığın neden 1/8'e bu kadar yakın olduğunu, ancak tam olarak olmadığını açıklamaktadır. Bu olasılığın tam değeri, sonsuz kosinüs çarpımı integrali C2 bölü π ile verilir.

Tükenmiş harmonik seriler

Paydanın herhangi bir yerinde 9 rakamının yer aldığı tüm terimlerin çıkarıldığı tükenmiş harmonik serinin yakınsadığı ve değerinin 80'den küçük olduğu gösterilebilir. Aslında, herhangi bir basamak dizisini (herhangi bir tabanda) içeren tüm terimler çıkarıldığında seri yakınsar.

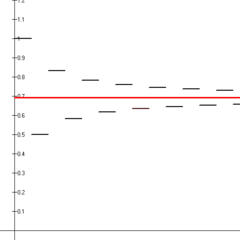
Değişken harmonik serilerin ilk on dört kısmi toplamının (siyah çizgi parçaları) 2'nin doğal logaritmasına (kırmızı çizgi) yakınsadığı gösterilmiştir.Zoom
Değişken harmonik serilerin ilk on dört kısmi toplamının (siyah çizgi parçaları) 2'nin doğal logaritmasına (kırmızı çizgi) yakınsadığı gösterilmiştir.

Uygulamalar

Harmonik seriler mantığa aykırı olabilir. Bunun nedeni, serinin terimleri küçülüp sıfıra doğru gitmesine rağmen ıraksak bir seri olmasıdır. Harmonik serinin ıraksaklığı bazı paradoksların kaynağıdır.

  • "Lastik banttaki solucan". Bir solucanın sonsuz elastikiyete sahip bir metrelik bir lastik bant boyunca, lastik bant düzgün bir şekilde gerilirken aynı anda süründüğünü varsayalım. Solucan dakikada 1 santimetre yol alırsa ve bant dakikada 1 metre gerilirse, solucan lastik bandın sonuna ulaşır mı? Cevap, mantığa aykırı bir şekilde "evet "tir, çünkü n dakika sonra solucanın kat ettiği mesafenin lastik bandın toplam uzunluğuna oranı şöyledir

1 100 ∑ k = 1 n 1 k . {\displaystyle {\frac {1}{100}}\sum _{k=1}^{n}{\frac {1}{k}}. } {\displaystyle {\frac {1}{100}}\sum _{k=1}^{n}{\frac {1}{k}}.}

Seri n büyüdükçe keyfi olarak büyüdüğünden, sonunda bu oran 1'i aşmalıdır, bu da solucanın lastik bandın sonuna ulaştığı anlamına gelir. Ancak, bunun gerçekleştiği n değeri son derece büyük olmalıdır: yaklaşık e100 , 1043 dakikayı (1037 yıl) aşan bir sayı. Harmonik seri sapma gösterse de, bunu çok yavaş yapar.

  • Jeep problemi, sınırlı yakıt taşıma kapasitesine sahip bir arabanın güzergah boyunca yakıt damlaları bırakarak bir çölü geçmesi için ne kadar toplam yakıt gerektiğini sormaktadır. Aracın belirli bir yakıt miktarıyla gidebileceği mesafe, logaritmik olarak büyüyen harmonik serilerin kısmi toplamlarıyla ilgilidir. Ve böylece gerekli yakıt, istenen mesafe ile üstel olarak artar.
  • Blok istifleme problemi: Özdeş domino taşlarından oluşan bir koleksiyon verildiğinde, bunları bir masanın kenarına, düşmeden masanın kenarından sarkacak şekilde istiflemek mümkündür. Mantığa aykırı olan sonuç, çıkıntıyı istediğiniz kadar büyük yapacak şekilde istiflenebilmeleridir. Tabii yeterli sayıda domino taşı varsa.
  • Havuzun duvarına her dokunduğunda daha hızlı giden bir yüzücü. Yüzücü 10 metrelik bir havuzu 2 m/s hızla geçmeye başlar ve her geçişte hızına 2 m/s daha eklenir. Teoride, yüzücünün hızı sınırsızdır, ancak bu hıza ulaşmak için gereken havuz geçişi sayısı çok büyük olur; örneğin, ışık hızına ulaşmak için (özel göreliliği göz ardı ederek) yüzücünün havuzu 150 milyon kez geçmesi gerekir. Bu büyük sayının aksine, belirli bir hıza ulaşmak için gereken süre, belirli sayıda havuz geçişindeki serilerin toplamına bağlıdır:

10 2 ∑ k = 1 n 1 k . {\displaystyle {\frac {10}{2}}\sum _{k=1}^{n}{\frac {1}{k}}. } {\displaystyle {\frac {10}{2}}\sum _{k=1}^{n}{\frac {1}{k}}.}

Toplamın hesaplanması, ışık hızına ulaşmak için gereken sürenin sadece 97 saniye olduğunu göstermektedir.

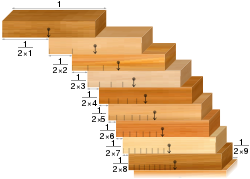
Blok istifleme problemi: Harmonik seriye göre hizalanmış bloklar herhangi bir genişlikteki yarıkları köprüler.Zoom
Blok istifleme problemi: Harmonik seriye göre hizalanmış bloklar herhangi bir genişlikteki yarıkları köprüler.

İlgili sayfalar

  • Harmonik ilerleme
  • Karşılıklı toplamların listesi

Sorular ve Yanıtlar

S: Harmonik seri nedir?


C: Harmonik seri, her bir terimin 1'e eşit olduğu ve dizideki konumuna bölündüğü sonsuz ıraksak bir seridir.

S: Bir serinin ıraksak olması ne anlama gelir?


C: Iraksak olması, daha fazla terim ekledikçe toplamın büyümesinin asla durmaması ve tek bir sonlu değere doğru gitmemesi anlamına gelir.

S: Bir serinin sonsuz olması ne anlama gelir?


C: Sonsuz, her zaman başka bir terim ekleyebileceğiniz ve serinin son teriminin olmadığı anlamına gelir.

S: Bu serinin adı nereden geliyor?


C: Bu serinin adı müzikteki harmonikler fikrinden gelir; burada üst tonların dalga boyları dizenin temel dalga boyunun 1/2, 1/3, 1/4, vb. kadardır.

S: Harmonik ortalama nedir?


C: Harmonik ortalama, bir dizideki her terimin komşu terimlerinin harmonik ortalamasına eşit olmasıdır. Bu ifade de müzikten gelmektedir.

S: Bu dizideki her bir terimi nasıl hesaplarız?


C: Bu dizideki her terim, birin dizideki konumuna bölünmesiyle hesaplanabilir (1/n).

AlegsaOnline.com - 2020 / 2023 - License CC3